Building an interpreter

Part 1: Lexing

To interpret source code, we must first convert it into a form that is easier to work with. This conversion starts with the lexer, also called tokenizer, which turns plaintext into a sequence of tokens.

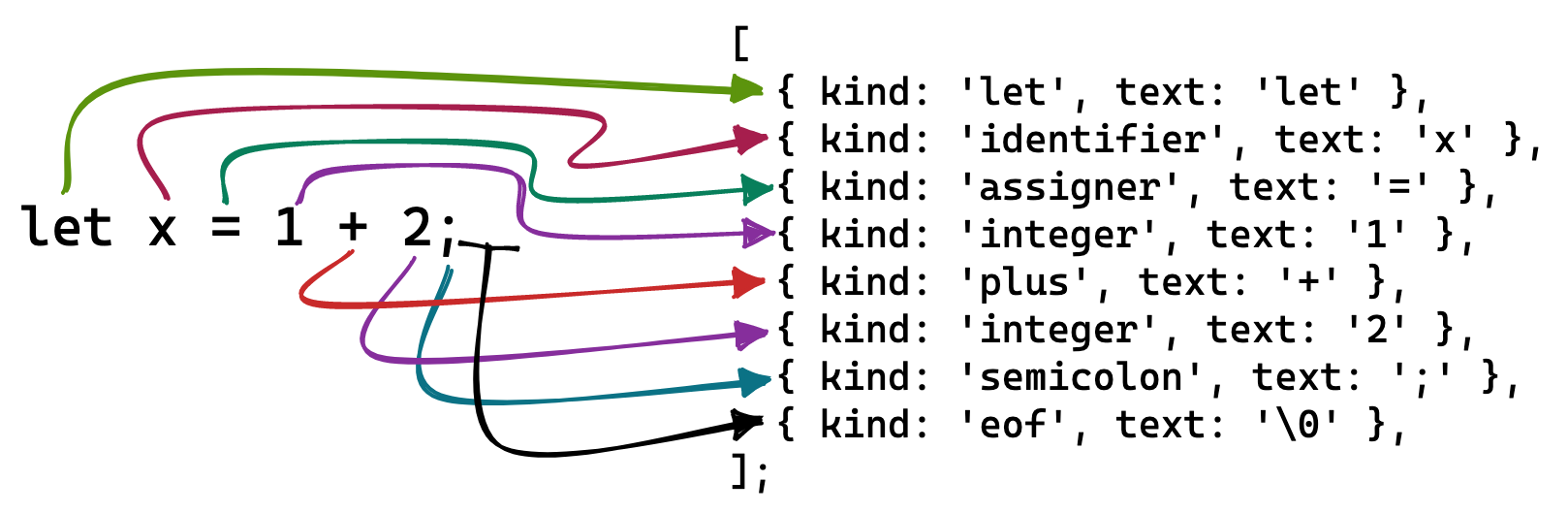
A lexer looks at each char in the input and produces tokens from them. This conversion can be 1:1 as in = → { kind: 'assigner', text: '=' } or n:1 as in let → { kind: 'let', text: 'let' }. Since a lexer analyzes each "lexeme" (unit) of the input, this process is called lexical analysis.

We begin by describing the structure of a token:

interface Token {
  kind: TokenKind;
  text: string;
}

type TokenKind = 'let' | 'identifier' | 'assigner'; // non-exhaustive

Let's first focus on Token['kind']. Broadly speaking, a token may be:

• language-defined, snippets of text given meaning by the creator of the language, e.g. keywords like let and operators like ==,
• user-defined, snippets of text given meaning by the user of the language, e.g. variable names like myVar and literals like 'hello', or
• special, tokens to cover special cases, e.g. illegal for unrecognizable tokens and eof for the end-of-file indicator.

Language-defined tokens can be subclassified based on the role they play in the language. For example, keywords reserve snippets of text for specific purposes (declaring a variable, declaring a function, etc.), operators are tokens that attach an operation to one or more values, and delimiters are tokens that separate tokens.

export type TokenKind =
  /**
   * Language-defined tokens
   */

	// keyword
  | 'let'
  | 'function'
	| 'if'
  | 'else'
  | 'return'

	// operator
  | 'assigner'
  | 'plus'
  | 'minus'
  | 'bang'
  | 'slash'
  | 'lessThan'
  | 'greaterThan'
  | 'asterisk'
	| 'equal'
	| 'notEqual';

	// delimiter
  | 'comma'
  | 'semicolon'
  | 'leftParen'
  | 'rightParen'
  | 'leftBrace'
  | 'rightBrace'

  /**
   * User-defined tokens
   */
  | 'identifier'
  | 'integer'

  /**
   * Special tokens
   */
  | 'illegal'
  | 'eof'

Remember, this is what a token looks like:

interface Token {
  kind: TokenKind;
  text: string;
}

Having looked at Token['kind'], we now turn to Token['text']. This is where we will store what the token looks like in the input plaintext.

For language-defined token types, Token['text'] is entirely predictable: when Token['kind'] is let, Token['text'] is always 'let', when Token['kind'] is leftParen, Token['text'] is always '('.

But for user-defined token types, Token['text'] is unpredictable: when Token['kind'] is identifier, Token['text'] will be whichever string the user decided on: 'myVar', 'myFunc', etc.

For special token types, when Token['kind'] is illegal, Token['text'] is the unrecognizable snippet of text, and when Token['kind'] is eof, Token['text'] contains an end-of-file indicator like \0, decided by the language author.

Now that we know about tokens, we can set up a process, the lexer, to read plaintext char by char and return a sequence of tokens from it.

We begin by creating a Lexer class:

class Lexer {
  /**
   * Plaintext provided to the lexer
   */
  input = '';

  /**
   * Current position in input
   */
  position = 0;

  /**
   * Char at current position in input
   */
  char = '';

  /**
   * Next position in input
   */
  peekPosition = 0;

  /**
   * Whether the lexer has finished reading the input,
   * i.e. whether it has reached the end-of-file indicator
   */
  finished = false;

  constructor(input: string) {
    this.input = input;
    this.readChar();
  }
}

input is the plaintext to tokenize. position is an index that stands for the current position of Lexer in the input. peekPosition is an index that stands for the next position to read. char is the character at the position under examination.

At the end of the lexer's constructor, we call its readChar() method:

class Lexer {
  // ...

  readChar() {
    if (this.peekPosition >= this.input.length) {
      this.char = '\0'; // edge case: end of file
    } else {
      this.char = this.input[this.peekPosition];
    }

    // move both pointers forward
    this.position = this.peekPosition;
    this.peekPosition += 1;
  }
}

In readChar(), we set the lexer's char field to the char at the lexer's next position, and then move both pointers forward. For the edge case of reaching the end of the source code, we choose to signal this with \0, i.e. ASCII for NUL.

Now that the lexer can both examine a char and move forward, we need a method to turn the char under examination into a token and continue moving forward:

class Lexer {
  // ...

  createToken() {
    let token: Token;

    switch (this.char) {
      case '=':
        token = { kind: 'assigner', text: '=' };
        break;
      case '!':
        token = { kind: 'bang', text: '!' };
        break;
      case '+':
        token = { kind: 'plus', text: '+' };
        break;
      case '-':
        token = { kind: 'minus', text: '-' };
        break;
      case '/':
        token = { kind: 'slash', text: '/' };
        break;
      case '*':
        token = { kind: 'asterisk', text: '*' };
        break;
      case '<':
        token = { kind: 'lessThen', text: '<' };
        break;
      case '>':
        token = { kind: 'greaterThen', text: '>' };
        break;
      case ';':
        token = { kind: 'semicolon', text: ';' };
        break;
      case ',':
        token = { kind: 'comma', text: ',' };
        break;
      case '(':
        token = { kind: 'leftParenthesis', text: '(' };
        break;
      case ')':
        token = { kind: 'rightParenthesis', text: ')' };
        break;
      case '{':
        token = { kind: 'leftBrace', text: '{' };
        break;
      case '}':
        token = { kind: 'rightBrace', text: '}' };
        break;
      case '\0':
        token = { kind: 'eof', text: '\0' };
        break;
      default: {
        token = { kind: 'illegal', text: this.char };
        break;
      }
    }

    // move to next char and advance both pointers
    this.readChar();

    return token;
  }
}

Note that createToken() currently can only tokenize single-char tokens like = and ; and +. What about letters or digits? A letter- or digit-based token may be made up of one char, as in 7 (integer) or x (identifier), or multiple chars, as in let (keyword) or myVar (identifier) or 123 (integer). Hence, when the char under examination is a letter or digit, we must continue reading until we have found the end of that token.

To do so, we append a default clause at the end of the switch statement:

switch (this.char) {
  // ...
  default: {
    if (isLetter(this.char)) {
      token = this.readText();
      return token;
    } else if (isNumber(this.char)) {
      token = this.readNumber();
      return token;
    } else {
      token = { kind: 'illegal', text: this.char };
      break;
    }
  }
}

If the char under examination is a letter, we find all the letters that together make up the multi-char token, and then find the token type for that literal. This will also work for single-char tokens.

class Lexer {
  // ...

  readText() {
    const start = this.position;

    // keep reading until we find a non-letter char
    while (isLetter(this.char)) this.readChar();

    // grab snippet of text
    const text = this.input.substring(start, this.position);

    // find token kind for snippet, which may be
    // lang-defined keyword or user-defined identifier

    // is it a lang-defined keyword?
    const keywords: { [key: string]: TokenKind } = {
      fn: 'function',
      let: 'let',
      true: 'true',
      false: 'false',
      if: 'if',
      else: 'else',
      return: 'return',
    };

    const kind = keywords[text];

    if (kind) return { kind, text };

    // if not a keyword, it must be a user-defined identifier
    return { kind: 'identifier', text };
  }

  readNumber() {
    const start = this.position;

    while (isNumber(this.char)) this.readChar();

    return {
      kind: 'integer',
      text: this.input.substring(start, this.position),
    };
  }
}

Look back at the createToken() method. What if we find whitespace? Think of or \n or \t. In the language we are parsing, as in many others, whitespace serves as a separator but is otherwise meaningless, so when tokenizing, we want to skip over whitespace - we do not want to return any token at all when encountering whitespace.

class Lexer {
  // ...

  createToken() {
    let token: Token;

    // consume whitespace
    while (isWhitespace(this.char)) this.readChar();

    switch (this.char) {
      case '=':
      // ...
    }
  }
}

Finally, to complete the lexer, we must take care of two special cases: the equality and inequality operators, i.e. == and !=. These are neither letters nor numbers and so require special treatment.

class Lexer {
  // ...

  createToken() {
    let token: Token;

    while (isWhitespace(this.char)) this.readChar();

    switch (this.char) {
      // ...
      case '=':
        if (this.peekChar() === '=') {
          this.readChar();
          token = { kind: 'equals', text: '==' };
        } else {
          token = { kind: 'assigner', text: '=' };
        }
        break;
      case '!':
        if (this.peekChar() === '=') {
          this.readChar();
          token = { kind: 'notEquals', text: '!=' };
        } else {
          token = { kind: 'bang', text: '!' };
        }
        break;
      // ...
    }
  }

  peekChar() {
    if (this.peekPosition >= this.input.length) return '\0';

    return this.input[this.peekPosition];
  }

  readChar() {
    if (this.peekPosition >= this.input.length) {
      this.char = '\0';
    } else {
      this.char = this.input[this.peekPosition];
    }

    this.position = this.peekPosition;
    this.peekPosition += 1;
  }
}

In these new branches in the switch statement, we first peek ahead at the next char (without actually moving to it) using the peekChar() method. Only if the next char is the second half of a two-char token do we actually move to that next char and create a token made up of these two chars.

---

Part 2: Parsing

Plaintext has now become a series of tokens, what next?

We must now specify how tokens relate to each other so that it is clear which operation to perform on which group of tokens. Evaluation requires structuring the relationships of token groups.

Arranging our tokens into a structure, namely a tree, that shows how our tokens relate to each other - this is the purpose of the parser. While building up the tree, the parser checks that the sequence of tokens it receives can be turned into a valid tree, which is why parsing is also called syntactic analysis. Its output, the syntax tree, will be evaluated in the final stage.

Plaintext...

if (3 * 5 > 10) {
  return 'hello';
} else {
  return 'bye';
}

becomes a sequence of tokens...

[
  { kind: 'if', text: 'if' },
  { kind: 'leftParen', text: '(' },
  { kind: 'integer', text: '3' },
  { kind: 'multiplier', text: '*' },
  { kind: 'integer', text: '5' },
  { kind: 'greaterThan', text: '>' },
  { kind: 'integer', text: '10' },
  { kind: 'rightParen', text: ')' },
];

which becomes a tree...

{
  type: "if-statement",
  condition: {
    type: "operator-expression",
    operator: ">",
    left: {
      type: "operator-expression",
      operator: "*",
      left: { type: "integer-literal", value: 3 },
      right: { type: "integer-literal", value: 5 }
    },
    right: { type: "integer-literal", value: 10 }
  },
  consequence: {
    type: "return-statement",
    returnValue: { type: "string-literal", value: "hello" }
  },
  alternative: {
    type: "return-statement",
    returnValue: { type: "string-literal", value: "bye" }
  }
}

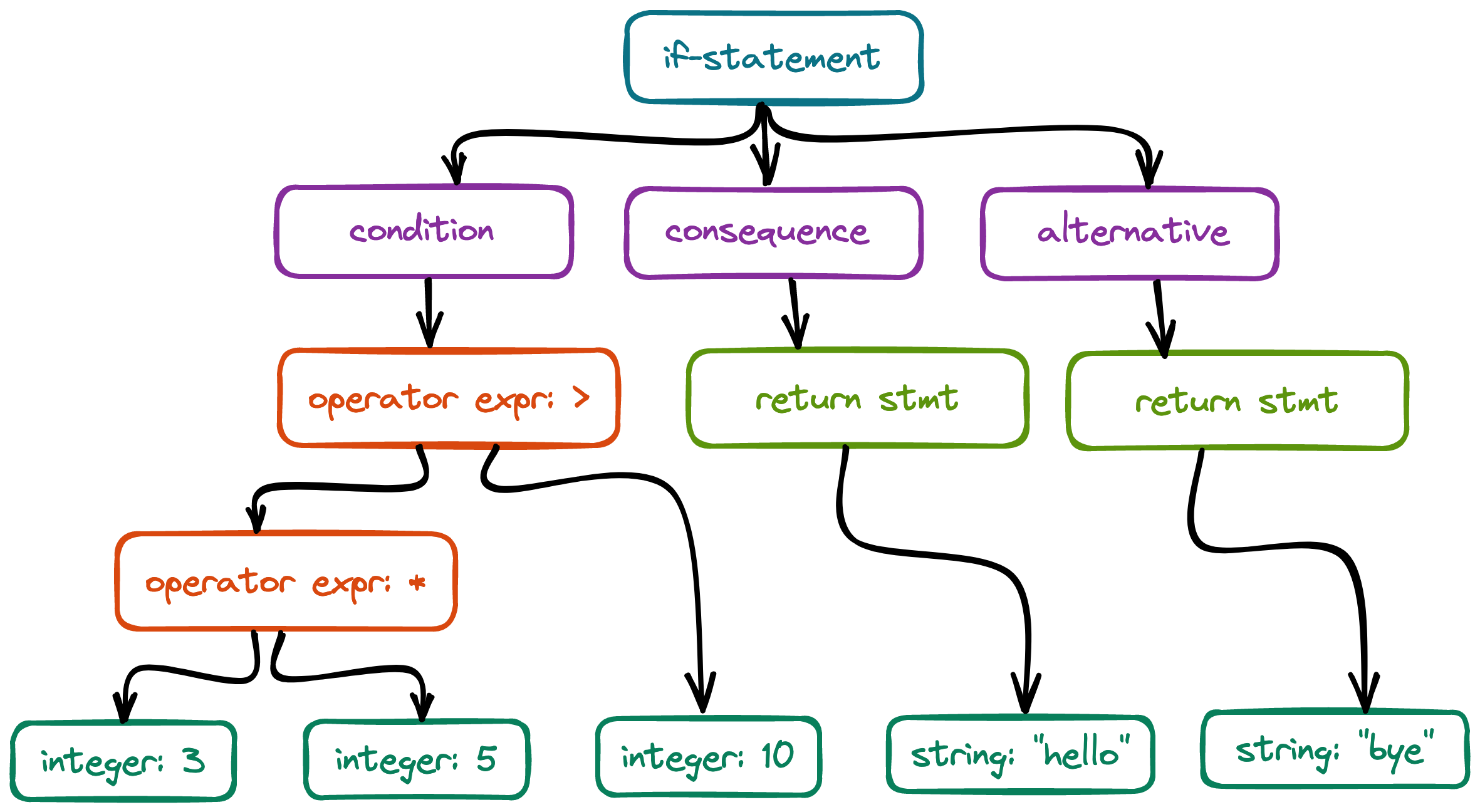
We can parse either top down or bottom up, i.e. we can create the topmost node and then recursively traverse its children downward, or we can start at the leaves of the tree and work our way upward to the topmost node.

In this implementation, we opt for a top-down parser, specifically a recursive descent parser, more specifically a top-down operator precedence parser, also known as a Pratt parser.

We begin with a one-line program:

let x = 5;

Lexically:

[
  { kind: 'let', text: 'let' },
  { kind: 'identifier', text: 'x' },
  { kind: 'assigner', text: '=' },
  { kind: 'integer', text: '5' },
];

Syntactically:

Program
	LetStatement
		name: Identifier: x
		expression: IntegerLiteral: 5

Remember: an expression always produces a value, e.g. 2 + 3, but a statement does not, e.g. let x = 2 + 3. The above one-line program is a statement declaring an identifier x and assigning it the result of evaluating the expression 5, which resolves to the integer literal 5. The identifier and the expression are children of the LetStatement node, which is a child of the topmost Program node.

Our syntax tree is made up of three basic node types:

type Node = Program | Statement | Expression;

At the top we have the Program node:

interface Program {
  kind: 'program';
  body: Statement[];
}

A program is a series of statements, which may be of various kinds:

type Statement = LetStatement | ReturnStatement; // non-exhaustive

// let x = 123
interface LetStatement {
  kind: 'let';
  name: Identifier; // x
  value: Expression; // 123
}

// return "abc" + "def"
interface ReturnStatement {
  kind: 'returnStatement';
  returnValue: Expression; // "abc" + "def"
}

As children of statements we often find expressions, also of various kinds:

type Expression =
  | Identifier
  | IntegerLiteral
  | BooleanLiteral
  | FunctionLiteral
  | UnaryExpression
  | BinaryExpression
  | IfExpression
  | CallExpression; // non-exhaustive

// x
interface Identifier {
  kind: 'identifier';
  value: string;
  x;
}

// 123
interface IntegerLiteral {
  kind: 'integerLiteral';
  value: number; // 123
}

// true
interface BooleanLiteral {
  kind: 'booleanLiteral';
  value: boolean; // true
}

// fn(x, y) { x + y; }
interface FunctionLiteral {
  kind: 'functionLiteral';
  parameters: Identifier[]; // x, y
  body: BlockStatement; // { x + y; }
}

// !x
interface PrefixExpression {
  kind: 'prefixExpression';
  operator: string; // !
  right: Expression; // x
}

// 1 + 2
interface BinaryExpression {
  kind: 'binaryExpression';
  operator: string; // +
  left: Expression; // 1
  right: Expression; // 2
}

// sum(1, 2)
interface CallExpression {
  kind: 'callExpression';
  func: Identifier | FunctionLiteral; // sum
  args: Expression[]; // 1, 2
}

// if (x > y) { "hi" } else { "bye" }
interface IfExpression {
  kind: 'ifExpression';
  condition: Expression; // x > y
  consequence: BlockStatement; // { "hi" }
  alternative?: BlockStatement; // { "bye" }
}

Graphically:

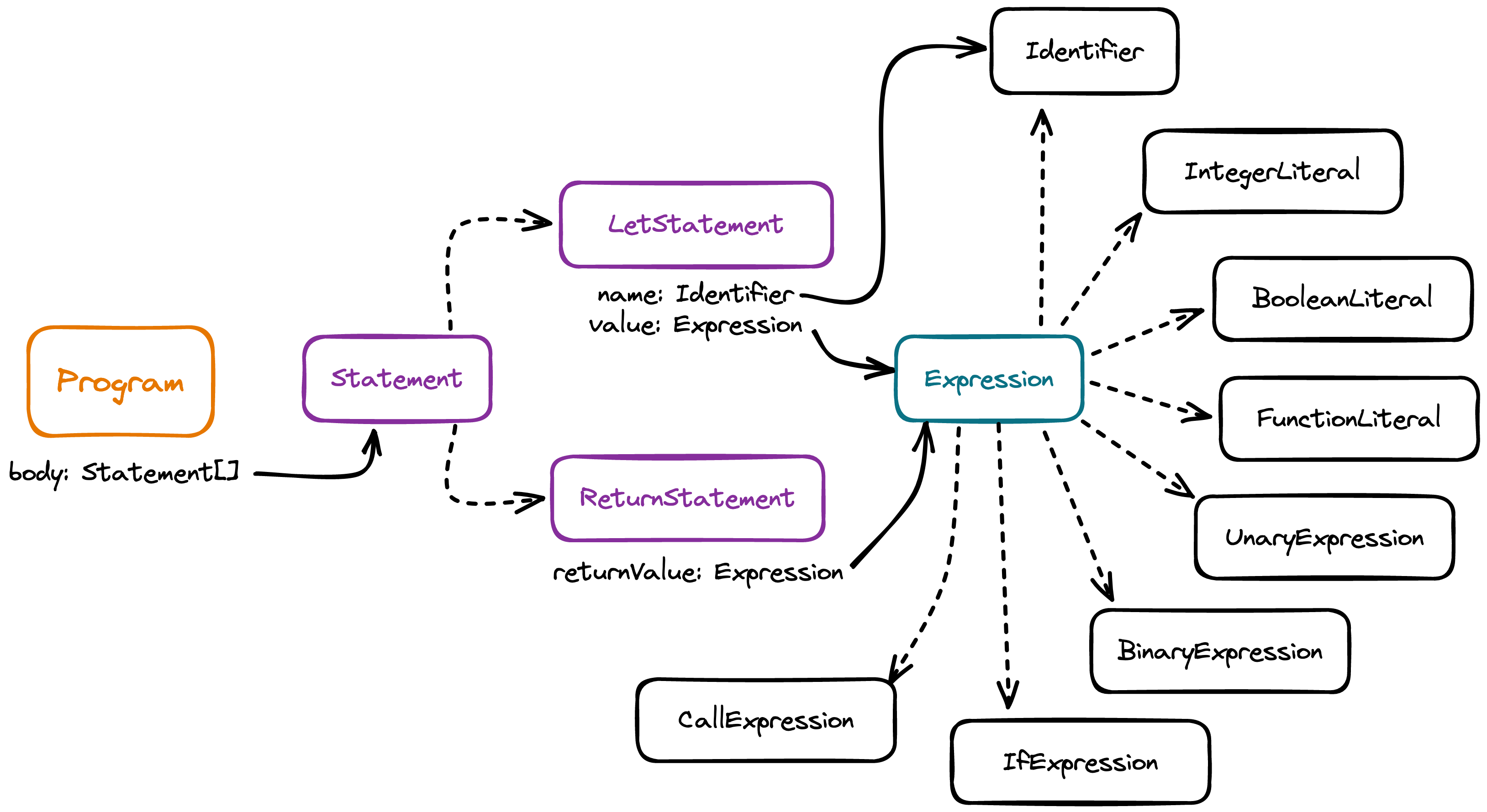
Now that we know what the output tree should look like, we can start writing the parser. We begin by setting up the lexer and two pointers.

class Parser {
	/**
	 * Instance of the lexer we created above
	 */
  lexer: Lexer;

	/**
	 * Current token under examination
	 */
  currentToken: Token;

	/**
	 * Next token to be examined
	 */
  peekToken: Token;

  constructor(lexer: Lexer) {
    this.lexer = lexer;

    this.currentToken = lexer.createToken(); // zeroth token
    this.peekToken = lexer.createToken(); // first token
  }

Next, we write the parser's main method parse to turn a series of tokens into an array of statements, which we return in a property of the topmost Program node.

class Parser {
  // ...

  parse() {
    const statements: ast.Statement[] = [];

    while (this.currentToken.kind !== 'eof') {
      // parse the current token into a statement
      const statement = this.parseStatement();

      if (statement) statements.push(statement);

      this.nextToken();
    }

    // build a `Program` node containing the collected statements
    return astBuilder.program(statements);
  }

  nextToken() {
    if (!this.peekToken) {
      throw new Error('No more tokens');
    }

    this.currentToken = this.peekToken;
    this.peekToken = this.lexer.createToken();
  }
}

Note that currentToken and peekToken in the parser behave much like position and peekPosition in the lexer, but here for tokens instead of chars. This is because, when we are parsing, we also need to peek ahead to decide what to do next. For example, if we encounter a 5, we will need to peek ahead to know if this is a single-char expression or rather the start of an arithmetic expression.

Parsing a program means parsing its statements, and parsing statements means parsing all kinds of statements. Hence we define a parseStatement method that dispatches to the appropriate parsing method based on the current token, and each parsing method validates the group of tokens and constructs a node from it.

class Parser {
  // ...

  parseStatement() {
    switch (this.currentToken.kind) {
      case 'let':
        return this.parseLetStatement(); // let x = 5;
      case 'return':
        return this.parseReturnStatement(); // return 5;
      default:
        return this.parseExpressionStatement(); // 5;
    }
  }

  parseLetStatement() {
    if (!this.expectPeek('identifier')) return;

    const name = astBuilder.identifier(this.currentToken.text);

    if (!this.expectPeek('assigner')) return;

    this.nextToken();

    const expression = this.parseExpression(Precedence.Lowest);

    if (!expression) throw new Error('Expected new expression');

    while (!this.currentTokenIs('semicolon')) this.nextToken();

    return astBuilder.letStatement(name, expression);
  }

  parseReturnStatement() {
    this.nextToken();

    const expression = this.parseExpression(Precedence.Lowest);

    if (!expression) throw new Error('Expected expression');

    while (!this.currentTokenIs('semicolon')) this.nextToken();

    return astBuilder.returnStatement(expression);
  }

  parseExpressionStatement() {
    const expression = this.parseExpression(Precedence.Lowest);

    if (!expression) return undefined;

    // expression statement is not announced by a keyword
    // so adjust the condition to identify the token range
    while (this.peekTokenIs('semicolon')) this.nextToken();

    return astBuilder.expressionStatement(expression);
  }
}

Note that each of these three nodes has an expression field. Hence the next call we need to understand is parseExpression(). This method is the heart of the Pratt parser.

Pratt parser

So far, we have parsed by processing tokens from left to right, validating them as we encounter them, and returning a node made up of the tokens that we expect.

Consider, however, the following challenges:

• Positioning: How will we handle tokens of the same type that have different effects in different positions? For example, in -5 - 10, the first - token is a unary operator that makes the 5 negative, and the second - token is a binary operator that applies subtraction to the two operands. Parsing must respect operator position.
• Nesting: How will we handle nesting? For example, in 5 * 5 + 10;, we want 5 * 5 to be nested, i.e. we want multiplication to happen before addition. Parsing must respect operator precedence.

A Pratt parser solves both problems.

To solve the positioning issue, i.e. to handle tokens of the same type differently depending on their position, a Pratt parser associates a token type with up to two parsing functions: one for when the token is found in prefix position like -1 and another for when the token is found in an infix position like 3 - 2.

class Parser {
  // ...

  prefixParseFunctions = new Map<TokenKind, PrefixParseFn>([
    ['minus', this.parseUnaryExpression.bind(this)],
    ['integer', this.parseIntegerLiteral.bind(this)],
    // and many others
  ]);

  infixParseFunctions = new Map<TokenKind, InfixParseFn>([
    ['minus', this.parseBinaryExpression.bind(this)],
    ['multiply', this.parseBinaryExpression.bind(this)],
    // and many others
  ]);

minus is associated with two parsing functions based on its position in the expression. integer and multiply are associated with one parsing function each.

With these parsing functions, we can now define the parseExpression() method to build the expression node:

class Parser {
  // ...

  parseExpression(precedence: Precedence) {
    /**
     * Implementation ellided for now. We are building to it.
     */
  }

  parseUnaryExpression() {
    const operator = this.currentToken.text;

    this.nextToken();

    const right = this.parseExpression(Precedence.Unary);

    if (!right) return;

    return astBuilders.unaryExpression(operator, right);
  }

  parseBinaryExpression(left: ast.Expression) {
    const operator = this.currentToken.text;

    const precedence = this.currentPrecedence();

    this.nextToken();

    const right = this.parseExpression(precedence);

    if (!right) return;

    return astBuilders.binaryExpression(operator, left, right);
  }
}

As soon as we come across an expression, we look at the token type, so we can tell operator position and call the appropriate parsing function. For example, in -5 - 10, we will first call parseUnaryExpression for the -5 expression, and then parseBinaryExpression for the LO - 10 expression. LO stands for left operand and is the expression node that was returned by parseUnaryExpression. For a binary expression like 5 - 10, the prefix parsing function will have created an integer literal node as the left operand of the binary expression.

This is why parseBinaryExpression takes an argument. By the time we call it, the left operand of the binary expression node has been parsed and will be uased as the left operand of the binary expression. For example, in -5 - 10, by the time we call parseBinaryExpression, we have already parsed -5 into a node and can use it as the left side of the binary expression we are about to parse.

Notice also the references to precedence in the implementation.

To solve the nesting issue, a Pratt parser associates token types, most often operators, with precedences, that is, how early their expression should be parsed - and therefore, how deeply nested the node should be in the tree. For example, in 5 * 5 + 10, we want 5 * 5 to be parsed before 5 + 10, i.e. we want 5 * 5 to be more deeply nested in the tree. In other words we want to afford * higher precedence than +.

We express precedences in integers so we can compare them - the higher the integer, the higher the precedence.

export enum Precedence {
  Lowest = 0,
  Equal = 1, // ==
  LessGreater = 2, // < or >
  SumSub = 3, // + or -
  MultiplyDivide = 4, // * or /
  Unary = 5, // -x or !x
  Call = 6, // (
}

Precedences are associated with token types:

export const precedenceMap = new Map<TokenKind, number>([
  ['equal', Precedence.Equal],
  ['notEqual', Precedence.Equal],
  ['lessThan', Precedence.LessGreater],
  ['greaterThan', Precedence.LessGreater],
  ['plus', Precedence.SumSub],
  ['minus', Precedence.SumSub],
  ['divide', Precedence.MultiplyDivide],
  ['multiply', Precedence.MultiplyDivide],
  ['leftParen', Precedence.Call],
]);

We also define two methods to find the precedence of the current and next tokens:

class Parser {
  // ...

  currentPrecedence() {
    const precedence = precedenceMap.get(this.currentToken.kind);

    return precedence ?? Precedence.Lowest;
  }

  peekPrecedence() {
    const precedence = this.peekToken && precedenceMap.get(this.peekToken.kind);

    return precedence ?? Precedence.Lowest;
  }
}

Remember, we are interested in precedence because we want an expression with multiple operators to be parsed correctly, with nesting where appropriate.

This two-operator expression...

1 * 2 + 3;

should become this tree:

Program
	ExpressionStatement
		BinaryExpression
			left: BinaryExpression
				left: IntegerLiteral: 1
				operator: *
				right: IntegerLiteral: 2
			operator: +
			right: IntegerLiteral: 3

Now that all the pieces are in place, we can finally write the parseExpression() method:

class Parser {
  // ...

  parseExpression(precedence: Precedence) {
    // Find the prefix parsing function for the current token kind.
    const prefixParseFn = this.prefixParseFunctions.get(this.currentToken.kind);

    if (!prefixParseFn) {
      this.errors.push(`No unary parse function for ${this.currentToken.kind}`);
      return;
    }

    // Call the prefix parsing function to build the expression node.
    let leftExpression = prefixParseFn();

    // Check if the expression continues with a binary operator and,
    // if so, for as many times as needed, find and call the binary
    // parsing function, adding to the current expression node.
    while (
      !this.peekTokenIs('semicolon') &&
      precedence < this.peekPrecedence()
    ) {
      const peekKind = this.peekToken?.kind;

      if (!peekKind) throw new Error('peekKind cannot be null.');

      const infixParseFn = this.infixParseFunctions.get(peekKind);

      if (!infixParseFn) return leftExpression;

      this.nextToken();

      if (!leftExpression) throw new Error('Expected to find left expression');

      leftExpression = infixParseFn(leftExpression);
    }

    // Return the full final expression node.
    return leftExpression;
  }
}

The loop in parseExpression() checks if the expression has not finished (i.e. no semicolon) and tries to find the infix parsing function for every token we consume. If we find one, we call it, passing in the expression returned by the prefix parsing function as the argument. And thanks to the second condition, precedence < this.peekPrecedence() we continue consuming tokens until we find one that has higher precedence.

Let's walk through an example.

How do we parse this program...

1 * 2 + 3;

into this tree...?

Program
	ExpressionStatement
		BinaryExpression
			left: BinaryExpression
				left: IntegerLiteral: 1
				operator: *
				right: IntegerLiteral: 2
			operator: +
			right: IntegerLiteral: 3

We begin by calling parseExpressionStatement(), which delegates to...

class Parser {
  parseExpression(precedence: Precedence) {
    const prefixParseFn = this.prefixParseFunctions.get(this.currentToken.kind);

    if (!prefixParseFn) {
      this.errors.push(`No unary parse function for ${this.currentToken.kind}`);
      return;
    }

    let leftExpression = prefixParseFn();

    // <loop>

    return leftExpression;
  }
}

Our token pointers are at these positions:

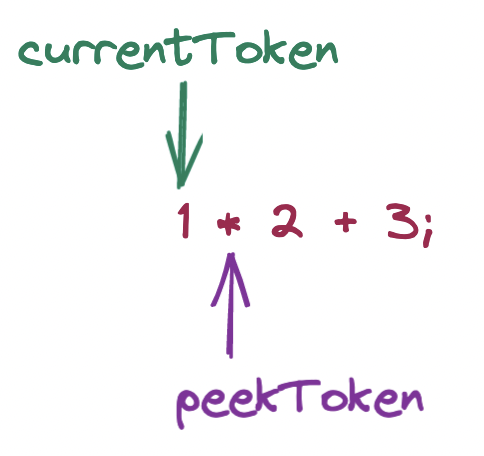
At parseExpression(), we check for a prefix parsing function associated with the current token type, the integer token for 1. We receive parseIntegerLiteral and call it, which returns an IntegerLiteral node, which we assign to leftExpression.

Then we loop:

// loop inside parseExpression()

while (!this.peekTokenIs('semicolon') && precedence < this.peekPrecedence()) {
  const peekKind = this.peekToken?.kind;

  if (!peekKind) throw new Error('peekKind cannot be null.');

  const infixParseFn = this.infixParseFunctions.get(peekKind);

  if (!infixParseFn) return leftExpression;

  this.nextToken();

  if (!leftExpression) throw new Error('Expected to find left expression');

  leftExpression = infixParseFn(leftExpression);
}

peekPrecedence (i.e. that of the * token) is higher than the argument passed to parseExpression, which was Precedence.Lowest, so we enter the loop. We retrieve the infix parsing function for the current token type, again the integer token for 1, and receive parseBinaryExpression. Before calling it and assigning its return value to leftExpression, we move forward the tokens, which now look like this:

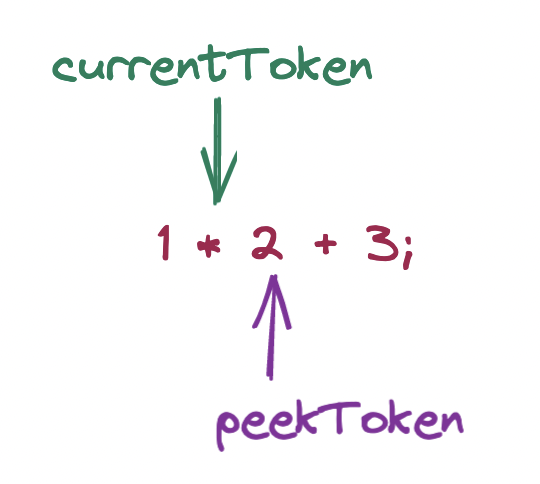
We now call parseBinaryExpression() and pass in the already parsed IntegerLiteral node for 1, i.e. the left side of the binary expression being built.

As a refresher:

class Parser {
  // ...

  parseBinaryExpression(left: ast.Expression) {
    const operator = this.currentToken.text;

    const precedence = this.currentPrecedence();

    this.nextToken();

    const right = this.parseExpression(precedence);

    if (!right) return;

    return astBuilders.binaryExpression(operator, left, right);
  }
}

parseBinaryExpression saves the current precedence (i.e. that of the * token), moves forward the tokens and calls parseExpression with this precedence. So parseExpression is called another time, with the token pointers looking like this:

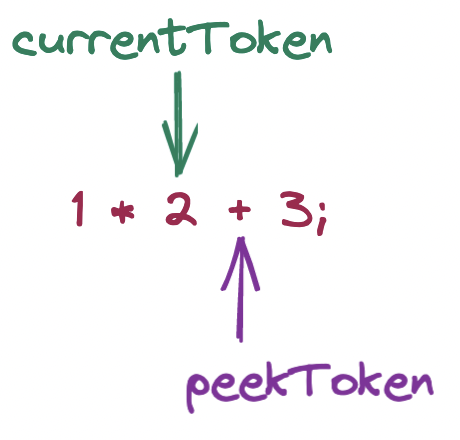
Once again, parseExpression looks for a prefix parsing function for the current token, which once again is parseIntegerLiteral. But this time, the condition of the for loop evaluates to false, because the precedence argument (i.e. of the * operator) is not smaller than the precedence of the current token (i.e. of the + operator). Rather, * has higher precedence. Hence, this time we skip the for loop and the IntegerLiteral node is returned.

We have built this nested binary expression:

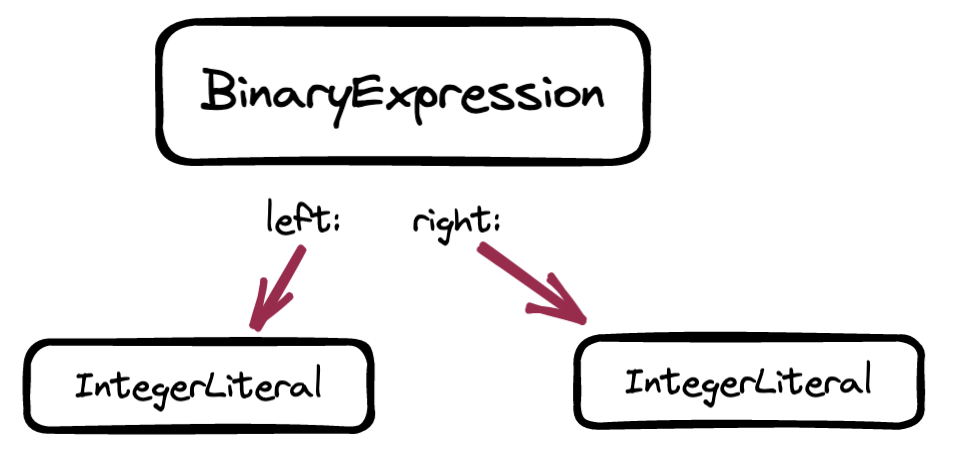
parseBinaryExpression returns this BinaryExpression node and we return to the original call to parseExpression, back where we started, where precedence remains at Precedence.Lowest. We evaluate the condition of the for-loop again: precedence < this.peekPrecedence()

This again evaluates to true, since precedence is Precedence.Lowest and peekPrecedence is now the precedence of the + operator, which is higher. We execute the for loop a second time, now with leftExpression as the BinaryExpression node for 1 * 2. The same procedure repeats: we fetch the infixParseFunction, which is parseBinaryExpression, which returns a BinaryExpression node, with the left side as our previous BinaryExpression and the right side with the final IntegerLiteral node for 3.

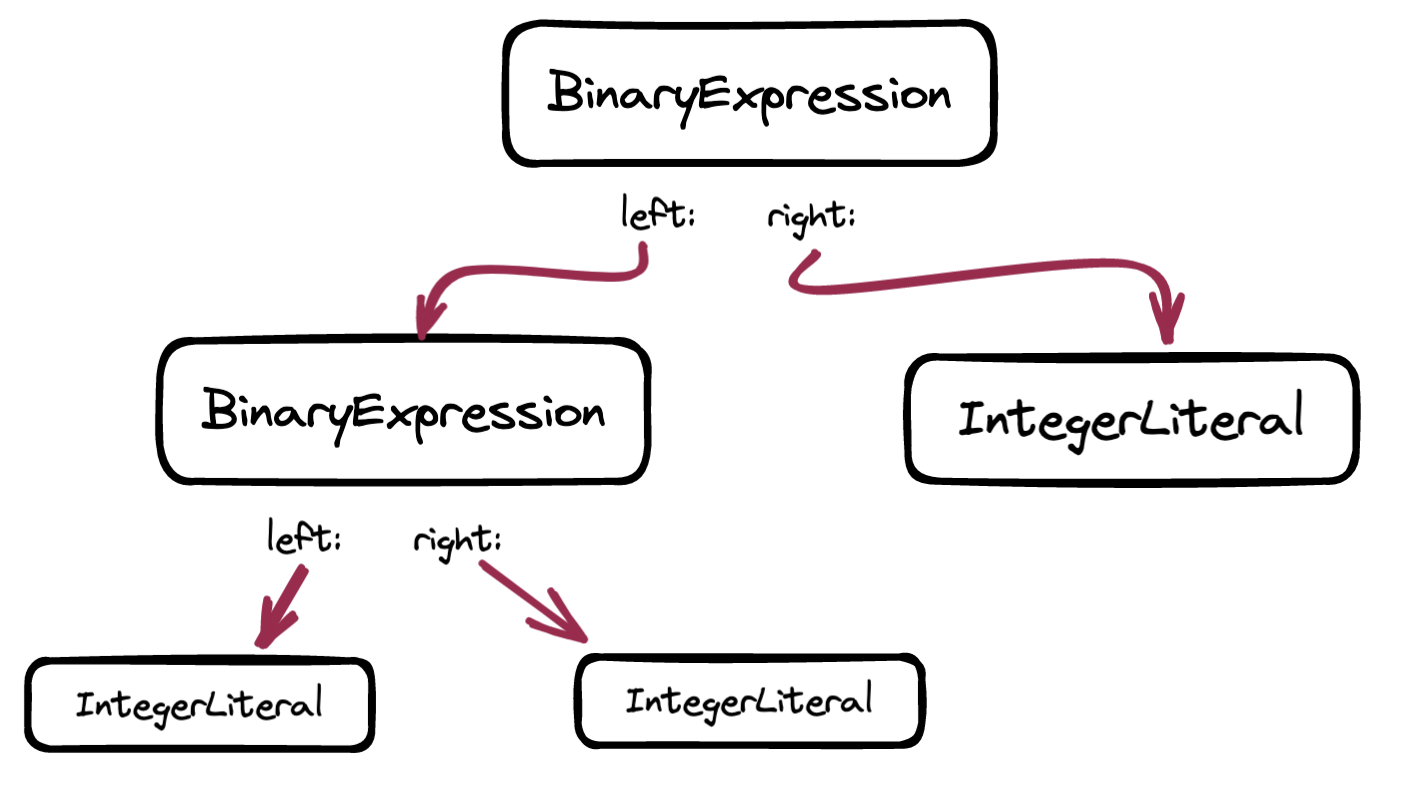
With the token pointers in these positions:

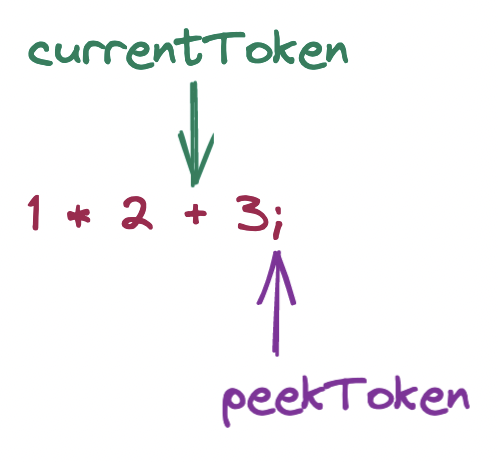
Since the next token is the semicolon, we skip the for loop and return the result accumulated in leftExpresison.

It all comes down to the condition precedence < this.peekPrecedence(), which checks if the associativity of the next token. If the associativity of the next token is higher, what we have parsed so far becomes part of, i.e. nested in, the node for the next token, from left to right, by being passed as an argument to its infix parsing function.

---

Part 3: Evaluating

Having built up a syntax tree, we can now evaluate it to turn it into a result.

Our evaluator is a function that takes the topmost node of the tree, recursively traverses every child down to its leaves, and for each leaf returns a value representing the result. Since the process is recursive, each value is passed up to the caller, where the node kind determines what to do with the value, i.e. whether to use it as a final result or as an operand in a larger expression.

In sum, we face two tasks:

• recursive traversal of nodes, and
• internal representation of values.

Let's begin with the latter. What exactly is this value returned by the evaluator to represent the result? In our implementation, we will internally represent values as objects:

export type Object = Integer | Boolean | Null | Error | ReturnValue | Fn; // non-exhaustive

export type Integer = { kind: 'integer'; value: number };
export type Boolean = { kind: 'boolean'; value: boolean };
export type Null = { kind: 'null' };
export type ReturnValue = { kind: 'returnValue'; value: Object };
export type Error = { kind: 'error'; value: string };

This internal representation can be later expanded, but for now it contains enough building blocks so that we can start traversing the tree and using these objects as values. Remember, objects represent evaluation results that can be used as a final result or combined with other values to produce the final result.

To traverse the tree, we begin at its top region:

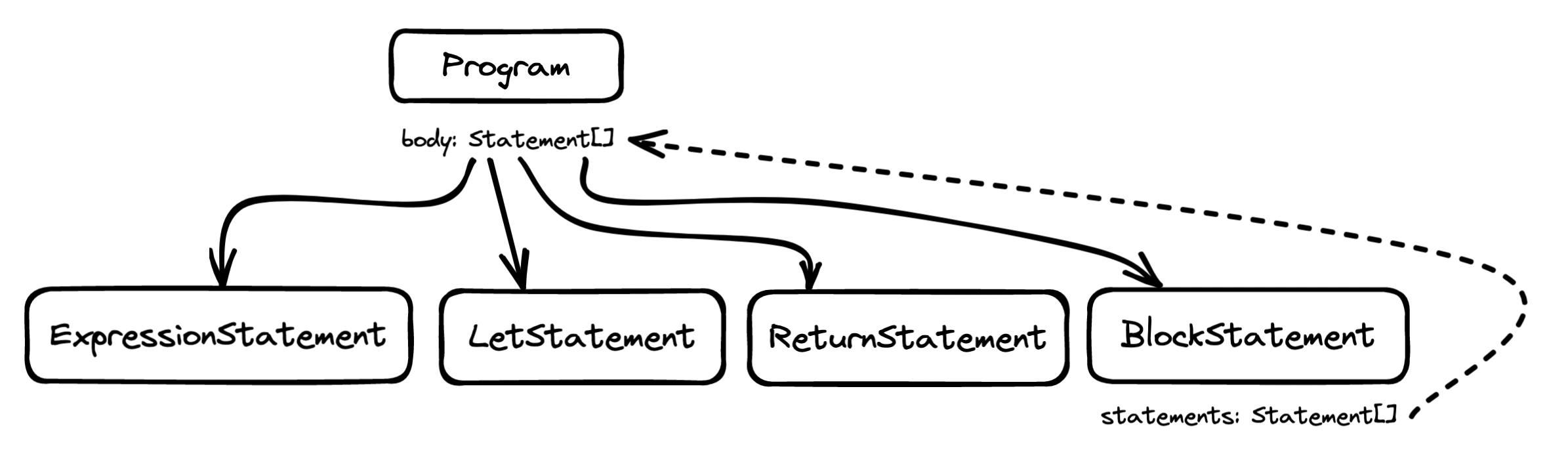
A Program is an array of statements and, in most cases, these do not contain further statements. The case that does contain further statements is a block of statements that eventually will be narrowed down to the majority case, i.e. statements that do not contain further statements.

Next, note how the majority case always holds a reference to an Expression:

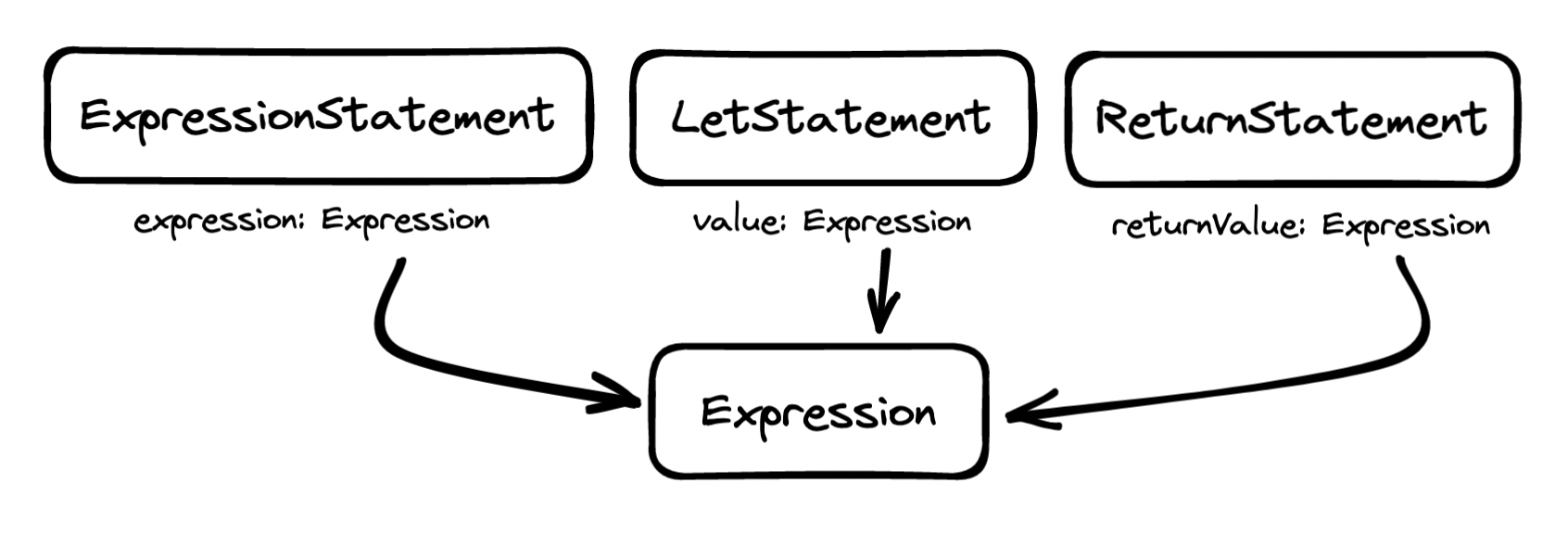
An expression statement is a statement is made up of an expression, as in 5;, a let statement binds the result of an expression to an identifier, as in x = 5; and a return statement designates the result of an expression as a return value, as in return 5;.

In turn, an Expression in the tree may be terminal or non-terminal:

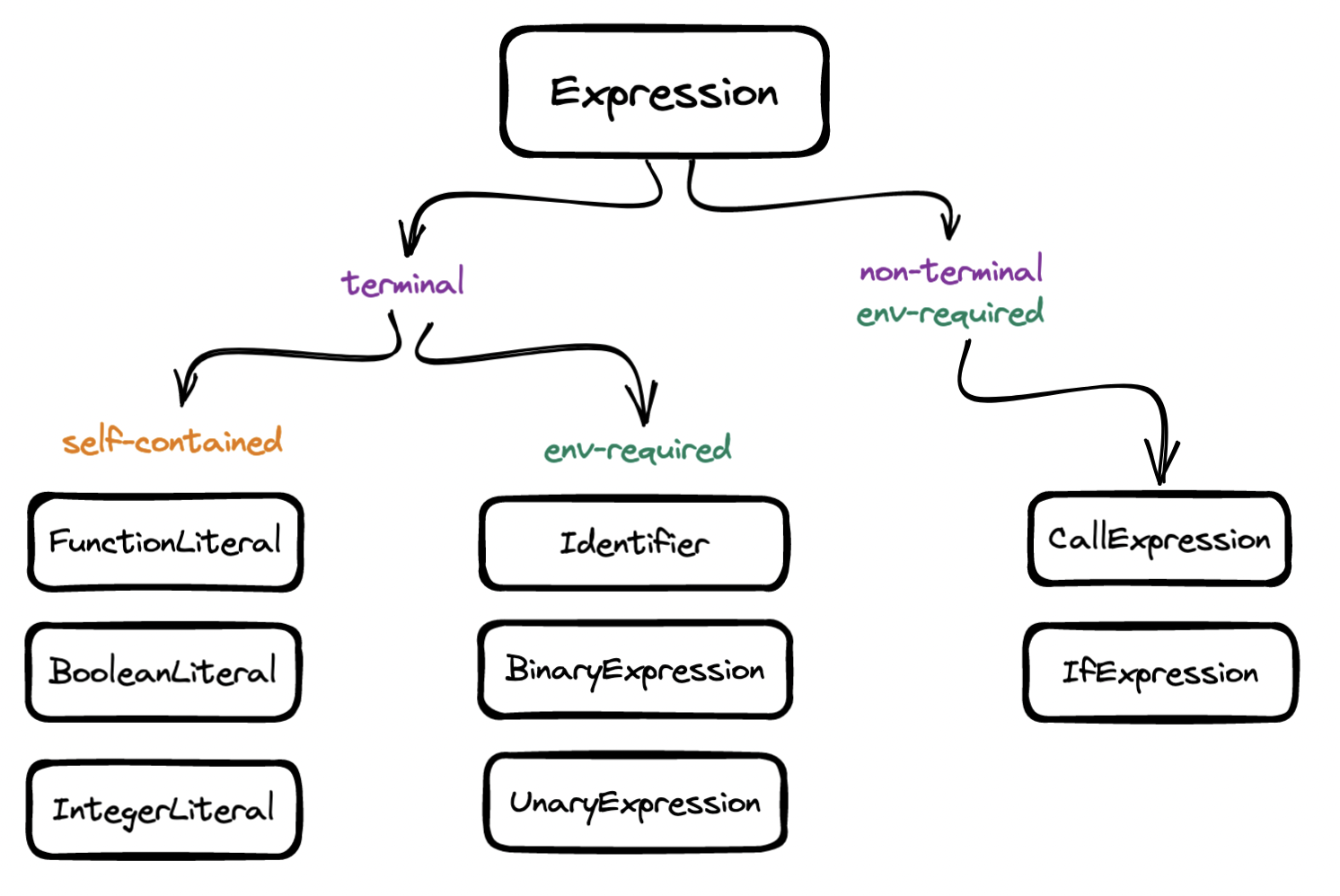
By terminal, we mean a node that can be turned into a value, e.g. we take a BooleanLiteral node and produce a Boolean value and so we do not need to keep traversing the tree - this is the majority case. By non-terminal, we mean a node that contains further nodes to traverse, i.e. we will have to keep recursing until we reach the terminal side of the tree.

Finally, note that the three of the terminal nodes are self-contained, i.e. evaluation does not require any further information. By contrast, in most cases, resolving an identifier like x or a unary expression like !y or a binary expression like z + 1 requires knowing the value associated with the identifier. That is, these expressions require access to the environment, or scope, to evaluate. Hence we will need to keep track of the contents of the scope as we evaluate env-required nodes.

We are now ready to implement the evaluator, starting with the dispatcher:

function evaluate(node: ast.Node, environment: env.Environment): obj.Object {
  switch (node.kind) {
    case 'program': {
      let result: obj.Object;

      for (const statement of program.body) {
        result = evaluate(statement, environment);

        if (result.kind === 'returnValue') {
          return result.value;
        } else if (result.kind === 'error') {
          return result;
        }
      }

      return result;
    }

    case 'blockStatement': {
      let result: obj.Object;

      for (const statement of node.statements) {
        result = evaluate(statement, environment);

        if (result.kind === 'returnValue' || result.kind === 'error') {
          return result;
        }
      }

      return result;
    }

    case 'expressionStatement': {
      return evaluate(node.expression, environment);
    }

    case 'letStatement': {
      const value = evaluate(node.value, environment);

      if (obj.isError(value)) return value;

      environment.set(node.name.value, value);

      return value;
    }

    case 'returnStatement': {
      const value = evaluate(node.returnValue, environment);

      if (obj.isError(value)) return value;

      return objBuilder.returnValue(value);
    }

    case 'integerLiteral': {
      return objBuilder.integer(node.value);
    }

    case 'booleanLiteral': {
      return objBuilder.boolean(node.value);
    }

    case 'functionLiteral': {
      return objBuilder.fn(node.parameters, node.body, environment);
    }

    case 'identifier': {
      return evaluateIdentifier(node, environment);
    }

    case 'unaryExpression': {
      const right = evaluate(node.right, environment);

      if (obj.isError(right)) return right;

      return evaluateUnaryExpression(node.operator, right);
    }

    case 'binaryExpression': {
      const left = evaluate(node.left, environment);

      if (obj.isError(left)) return left;

      const right = evaluate(node.right, environment);

      if (obj.isError(right)) return left;

      return evaluateBinaryExpression(node.operator, left, right);
    }

    case 'ifExpression': {
      return evaluateIfExpression(node, environment);
    }

    case 'callExpression': {
      const func = evaluate(node.func, environment);

      if (obj.isError(func)) return func;

      const args = evaluateExpressions(node.args, environment);

      if (args.length == 1 && obj.isError(args[0])) return args[0];

      return callFunction(func, args);
    }

    default:
      throw new Error(`unexpected node: '${node}'`);
  }
}

We keep recursing...

• to reach a terminal node that we evaluate to, e.g. a simple statement consisting of only a literal or identifier, or
• to find all the values we must combine with others for evaluation, e.g. a more complex statement consisting of a unary, binary, if or call expression.

function evaluateUnaryExpression(
  operator: string,
  right: obj.Object
): obj.Object {
  switch (operator) {
    case '!':
      return evaluateBangOperatorExpression(right);
    case '-':
      return evaluateMinusOperatorExpression(right);
    default:
      return obj.error(`unknown operator: ${operator}${right.kind}`);
  }
}

function evaluateBangOperatorExpression(right: obj.Object): obj.Object {
  switch (right.kind) {
    case 'boolean':
      return right.value ? obj.FALSE : obj.TRUE;
    case 'null':
      return obj.TRUE;
    default:
      return obj.FALSE;
  }
}

function evaluateMinusOperatorExpression(right: obj.Object): obj.Object {
  if (right.kind !== 'integer') {
    return obj.error(`unknown operator: -${right.kind}`);
  }

  return obj.integer(-right.value);
}

function evaluateBinaryExpression(
  operator: string,
  left: obj.Object,
  right: obj.Object
): obj.Object {
  if (left.kind !== right.kind) {
    return obj.error(`type mismatch: ${left.kind} ${operator} ${right.kind}`);
  }

  switch (operator) {
    case '==':
      return obj.boolean(obj.eq(left, right));
    case '!=':
      return obj.boolean(!obj.eq(left, right));
  }

  if (left.kind === 'integer' && right.kind === 'integer') {
    return evaluateIntegerBinaryExpression(operator, left, right);
  }

  return obj.error(`unknown operator: ${left.kind} ${operator} ${right.kind}`);
}

function evaluateIntegerBinaryExpression(
  operator: string,
  left: obj.Integer,
  right: obj.Integer
): obj.Object {
  switch (operator) {
    case '+':
      return obj.integer(left.value + right.value);
    case '-':
      return obj.integer(left.value - right.value);
    case '*':
      return obj.integer(left.value * right.value);
    case '/':
      return obj.integer(left.value / right.value);
    case '>':
      return obj.boolean(left.value > right.value);
    case '<':
      return obj.boolean(left.value < right.value);
    default:
      return obj.error(
        `unknown operator: ${left.kind} ${operator} ${right.kind}`
      );
  }
}

function evaluateIfExpression(
  node: ast.IfExpression,
  environment: env.Environment
): obj.Object {
  const condition = evaluate(node.condition, environment);

  if (obj.isError(condition)) return condition;

  if (obj.isTruthy(condition)) {
    return evaluate(node.consequence, environment);
  } else if (node.alternative) {
    return evaluate(node.alternative, environment);
  }

  return obj.NULL;
}

function evaluateCallExpression(
  node: ast.CallExpression,
  environment: env.environment
): obj.Object {
  const func = evaluate(node.func, environment);

  if (obj.isError(func)) return func;

  const args = evaluateExpressions(node.args, environment);

  if (args.length == 1 && obj.isError(args[0])) return args[0];

  if (func.kind !== 'fn') return obj.error('not a function: ' + func.kind);

  const extendedEnvironment = extendFunctionEnvironment(func, args);
  const evaluated = evaluate(func.body, extendedEnvironment);

  if (evaluated.kind === 'returnValue') return evaluated.value;

  return evaluated;
}

function extendFunctionEnvironment(
  func: obj.Fn,
  args: obj.Object[]
): env.Environment {
  const environment = new env.Environment(func.env);

  for (let p = 0; p < func.parameters.length; p++) {
    const { value } = func.parameters[p];
    const arg = args[p];

    environment.set(value, arg);
  }

  return environment;
}

Pay special attention to the environment.

We first create the environment and pass it to the dispatcher: evaluator.evaluate(program, new env.Environment()). Whenever we come across a let statement, we add the identifier-value pair to the environment: environment.set(identifier, value) and every time we evaluate an identifier, we retrieve the value from the environment: environment.get(identifier).

Also note that whenever we evaluate a function call, we add the existing environment to the outer section of the environment and we add the function parameters to the new environment. This way we can access variables from the outer scope, while giving precedence to function parameters.

class Environment {
  store: Map<string, obj.Object>;
  outer?: Environment;

  constructor(outer?: Environment) {
    this.store = new Map();
    this.outer = outer;
  }

  get(name: string): obj.Object | undefined {
    let obj = this.store.get(name);

    if (!obj) obj = this.outer?.get(name);

    return obj;
  }

  set(name: string, value: obj.Object): void {
    this.store.set(name, value);
  }
}

Pay also close attention to return values.

In the language we are implementing, we can return values from functions, and at the top level. In both cases, the return statement stops the evaluation of a series of statements and resolves to the value that its expression has evaluated to.

1 * 2 * 3; // executed
return 7; // result
4 + 5 + 6; // unexecuted

At the same time, consider that not all return statements values should stop evaluation:

if (10 > 1) {
  if (10 > 1) {
    return 10;
  }
  return 1;
}

In the above example, tree traversal will find return 1 (less deeply nested) before return 10 (more deeply nested). If we incorrectly stopped evaluation on the first return statement, we would never reach the second return statement.

To solve this issue, we wrap the return value:

function evaluate(node: ast.Node, environment: env.Environment): obj.Object {
  switch (node.kind) {
    // ...

    case 'returnStatement': {
      const value = evaluate(node.returnValue, environment);

      if (obj.isError(value)) return value;

      return objBuilder.returnValue(value); // { kind: 'returnValue', value }
    }
  }
}

We unwrap the return value when we evaluate a program:

function evaluate(node: ast.Node, environment: env.Environment): obj.Object {
  switch (node.kind) {
    case 'program': {
      let result: obj.Object;

      for (const statement of program.body) {
        result = evaluate(statement, environment);

        if (result.kind === 'returnValue') {
          return result.value; // unwrap
        } else if (result.kind === 'error') {
          return result;
        }
      }

      return result;
    }

    // ...
  }
}

And when we evaluate a function call expression:

function evaluateCallExpression(func: Value, args: Value[]): Value {
  if (func.kind !== 'fn') {
    return valueBuilders.error('not a function: ' + func.kind);
  }

  const fnEnv = env.Environment.createFunctionEnv(func, args);
  const evaluated = evaluate(func.body, fnEnv);

  if (evaluated.kind === 'returnValue') return evaluated.value;

  return evaluated;
}

But we avoid unwrapping it during evaluation of a block statement:

switch (node.kind) {
  // ...

  case 'blockStatement': {
    let result: obj.Object;

    for (const statement of node.statements) {
      result = evaluate(statement, environment);

      if (result.kind === 'returnValue' || result.kind === 'error') {
        return result;
      }
    }

    return result;
  }
}