Heaps and Tries

Heap

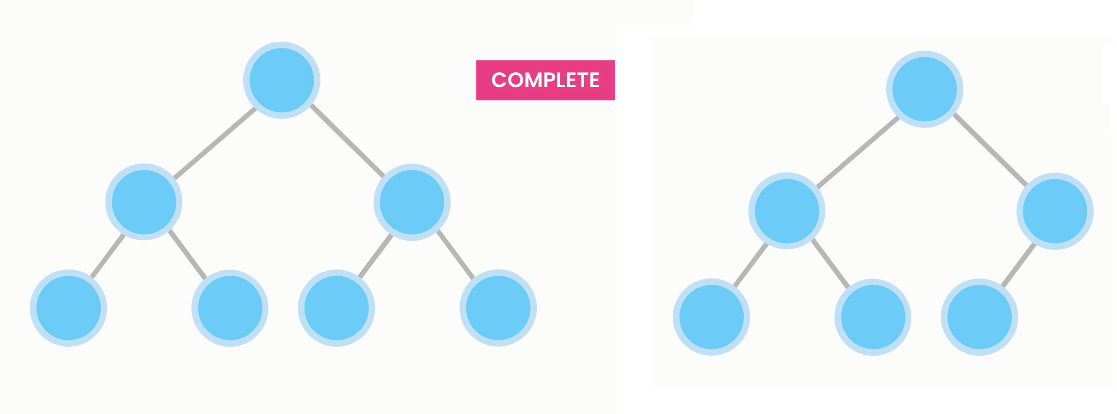
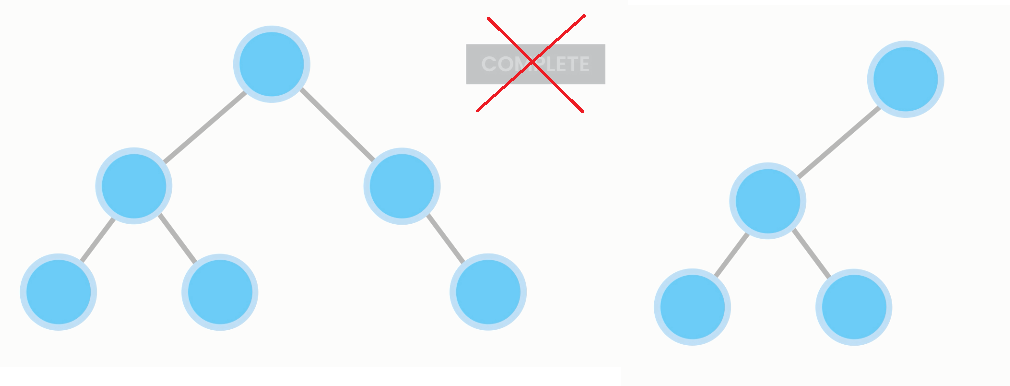
A heap is a type of tree with two properties: completion and heap property.

A heap is complete, i.e. every level is fully filled, or has nodes inserted consecutively from left to right.

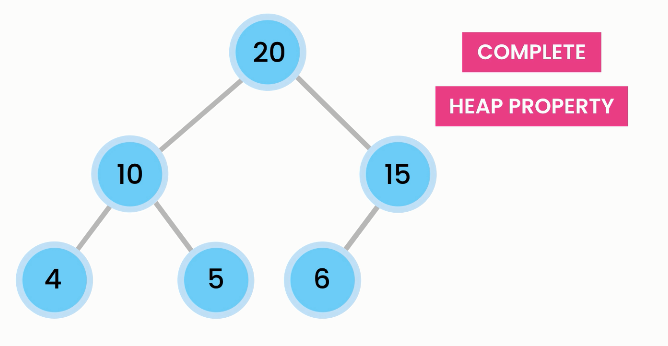
A heap has a heap property if the value of every node is greater (max heap) or smaller (min heap) than or equal to its children.

In a max heap, where the root value is the greatest, inserting a value that is larger than the current heap causes that value to bubble up and the former root value to bubble down.

Heaps are trees (usually binary trees) where (in a max heap) each child node has a value less than or equal to the parent node's value. (In a min-heap, each child is greater than or equal to its parent.) Consequently, the root node always has the largest value in the tree, which means that you can find the maximum value in constant time: simply return the root value. Insertion and deletion are still O(log n), but lookup becomes O(n).

Implementation

Since heaps are complete binary trees without holes in them, they can be implemented using an array, i.e. no separate Node class.

Formulas for calculating the indexes of the nodes of a heap:

• left = parent * 2 + 1
• right = parent * 2 + 1
• parent = (index - 1) / 2

Example implementation:

public class Heap {
    private int[] items = new int[10];
    private int size;

    public insert(int value) {
        // if capacity is full before insertion
        if (size == items.length)
            throw new IllegalStateException();

        // first, insert new item in next available slot
        items[size] = value;
        size++;

        // and then, if new item is greater than parent, bubble it up
        bubbleUp();
    }

    public void remove() {
        // no params because we always remove the root node

        // first, remove
        // node `--size` decrements value BEFORE using it as index
        items[0] = items[--size];

        // and then, if new item is smaller than parent, bubble it down
        // as long as it is not a valid parent
        var index = 0;
        while (index <= size && !isValidParent(index)) {
            var largerChildIndex = (leftChild(index) > rightChild(index)) ?
                                    leftChildIndex(index) :
                                    rightChildIndex(index);
            swap(index, largerChildIndex);
            index = largerChildIndex;
        }

    }

    private boolean isValidParent(int index) {
        return items[index] >= leftChild(index) && items[index] >= rightChild(index);
    }

    private int rightChild(int index) {
        return items[rightChildIndex(index)];
    }

    private int leftChild(int index) {
        return items[leftChildIndex(index)];
    }

    private int leftChildIndex(int index) {
        return index*2 + 1;
    }

    private int righttChildIndex(int index) {
        return index*2 + 2;
    }

    private void bubbleUp() {
        var indexOfLastItem = size - 1;
        var indexOfParent = (index - 1) / 2;
        while (index > 0 &&
            items[indexOfLastItem] > items[indexOfParent]) {
            swap(indexOfLastItem, indexOfParent);

            // now reset the index to keep bubbling up if necessary
            // set the index to its parent!
            index = (index - 1) / 2;
        }
    }

    private void swap(int first, int second) {
        var temp = items[first];
        items[first] = items[second];
        items[second] = temp;
    }
}

Trie

A trie (pronounced "try") provides superfast lookups for autocompletion. Trie comes from retrieval. Tries are also called digital, radix or prefix trees.

Why not arrays for autocompletion? 1. The search will be wasteful because word may have the same prefix. 2. It is slow because we have to check every item to see if the word starts with a prefix.

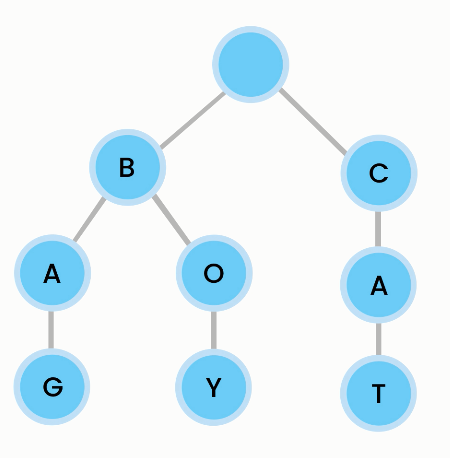
Note that the node is empty, because the beginning can be any letter. For each node, the trie asks "Does the node have a child for [letter]?". If so, it moves on to that node and asks again until the full word is found.

Lookups are O(L), that is, lookups are dependent on the length of the word being looked up. Same for insertions, deletions.

Implementation

Implementing a trie with an array:

public class Trie {
    public static int ALPHABET_SIZE = 26;

    private class Node {
        private char value;
        private Node[] children = new Node[ALPHABET_SIZE];
            // a char may be followed by any other child
            // the children of the node may be any letter in the alphabet
            // we create a node ARRAY to contain all possible children
            // see how to use a hash table (instead of an array) below
        private boolean isEndOfWord;
        public Node(char value) {
            this.value = value;
        }
        @Override
        public String toString() {
            return "value=" + value;
        }
    }
    private Node root = new Node(" ");

    public void insert(String word) {
        var current = root;
        for (var ch : word.toCharArray()) {
            var index = ch - "a";

            // if current node does not have this char
            if (current.children[index] == null)
                // create the node
                current.children[index] = new Node(ch);

            // grab a reference to that new node
            current = current.children[index];
        }
        // after loop, mark last node as end of word
        current.isEndOfWord = true;
    }
}

Implementing a trie with an hash table:

public class Trie {
    private class Node {
        private char value;
        private HashMap<Character, Node> children = new HashMap<>();
        // a hash table is more efficient because we are not initializing
        // an array with 26 items by defualt for each node
        private boolean isEndOfWord;
        public Node(char value) {
            this.value = value;
        }
        @Override
        public String toString() {
            return "value=" + value;
        }

    private Node root = new Node(" ");

    public void insert(String word) {
        var current = root;
        for (var ch : word.toCharArray()) {
            if (current.children.get(ch) == null)
                current.children.put(ch, new Node(ch));
            current = current.children.get(ch);
        }
        current.isEndOfWord = true;
    }

    public boolean contains(String word) {
        var current = root;
        for (var ch : word.toCharArray()) {
            if (!current.children.get(ch) == null)
                return false;
            current = current.children.get(ch);
        }
        // based on `isEndOfWord` because if you have stored only "care" and you are
        // looking up "car", you should get `false` since the word "car" is not stored
        return current.isEndOfWord;
    }

    public Node[] getChildren() {
        return children.values().toArray(new Node[0]);
    }
}

Trie traversal

You can traverse a trie in pre-order (root to leaf, to print words in a trie) or post-order (leaf to node, to remove word from a trie).

public void traversePreOrder(Node root) {
    // visit root first
    System.out.println(root.value);

    // and then each node and then its children nodes
    // remember: each node may have up to 26 children!
    for (var child : root.getChildren())
        // recurse on each child node of root node, and on each child node
        // of the children nodes of root node, and so on...
        traverse(child);
}

public void traversePostOrder(Node root) {
    // visit each leaf first and then its parent nodes
    // remember: each node may have up to 26 children!
    for (var child : root.getChildren())
        // recurse on each child node of root node, and on each child node
        // of the children nodes of root node, and so on...
        traverse(child);

    // and then root
    System.out.println(root.value);
}

Common operations

Removing a word from a trie

In a trie, to remove a smaller word that is part of a larger word, you toggle to false the isEndOfWord marker of the smaller word.

In a trie, to remove a larger word that is part of a smaller word, you toggle to false the isEndOfWord marker of the larger word, then you look at the children of the node that was the end of the larger word and, if there are no children, you recurse upwards and delete the node that was the end of the larger word over and over again.

public void remove(String word) {
    remove(root, word, 0);
}

private void remove(Node root, String word, int index) {
    // base condition: if visiting last letter of word
    if (index == word.length()) {
        System.out.println(root.value);
        root.isEndOfWord = false;
        return;
    }

    var ch = word.charAt(index);
    var child = root.children.get(ch);
    if (child == null)
        return;

    // recurse moving downward
    remove(child, word, index + 1);

    // if child has no children and is not the end of another word
    if (child.getChildren().length == 0 && !child.isEndOfWord) {
        root.removechild(ch);
    }
}

public void removeChild(char ch) {
    children.remove(ch);
}

Autocompletion with tries

Do a pre-order traversal, look only at the nodes that represent the prefix, check if the node represents the end of a word and, if so, add the word to the autocompletion list.

public List<String> findWords(String prefix) {
    List<String> words = new ArrayList<>();
    var lastNode = findLastNodeOf(prefix);
    findWords(lastNode, prefix, words);
    return words;
}

private void findWords(Node root, String prefix, List<String> words) {
    if (root.isEndOfWord)
        words.add(prefix);
    for (var child : root.getChildren())
        findWords(child, prefix + child.value, words);
}

private Node findLastNodeOf(String prefix) {
    var current = root;
    for (var ch : prefix.toCharArray()) {
        var child = current.children.get(ch);
        if (child == null)
            return null; // no prefix in trie
        current = child; // move on to child node
    }
    return current; // last node for prefix
}