Designing a typeahead search system

Typing into a search box and immediately seeing suggestions, also known as typeahead search, is a feature so common as to have become an expectation. Google, Twitter, GitHub, Amazon, YouTube, and many others all offer their own flavor of typeahead search—it is hard to imagine search without it.

Effortless as it seems, typeahead search is not trivial to implement at scale. Serving suggestions in the blink of an eye requires a system able to ingest, process, and store constantly changing data—and perhaps most importantly, to query it in milliseconds. How do we strike a balance between speed, relevance, and cost efficiency?

Let's design a typeahead search system.

Framing the design

From the user's perspective, typeahead search requires...

• Speed: As a user types their query, suggestions must be offered instantly, on every keypress, in the order of 100 milliseconds. Suggestions slower than the average typing speed would defeat the purpose of the feature.

• Relevance: Relevant suggestions are more likely to make for a successful search. Relevant suggestions are those based on the user's query and popular among other users, as indicated by how many times they have been searched for in the past.

Functionally, this means that our system must be able to accept user queries from a variety of sources (e.g. web, mobile, and desktop), process those queries into usable records (i.e. text and frequency), and store and serve those records while optimizing for reads. A starting point for the retrieval component might look like this:

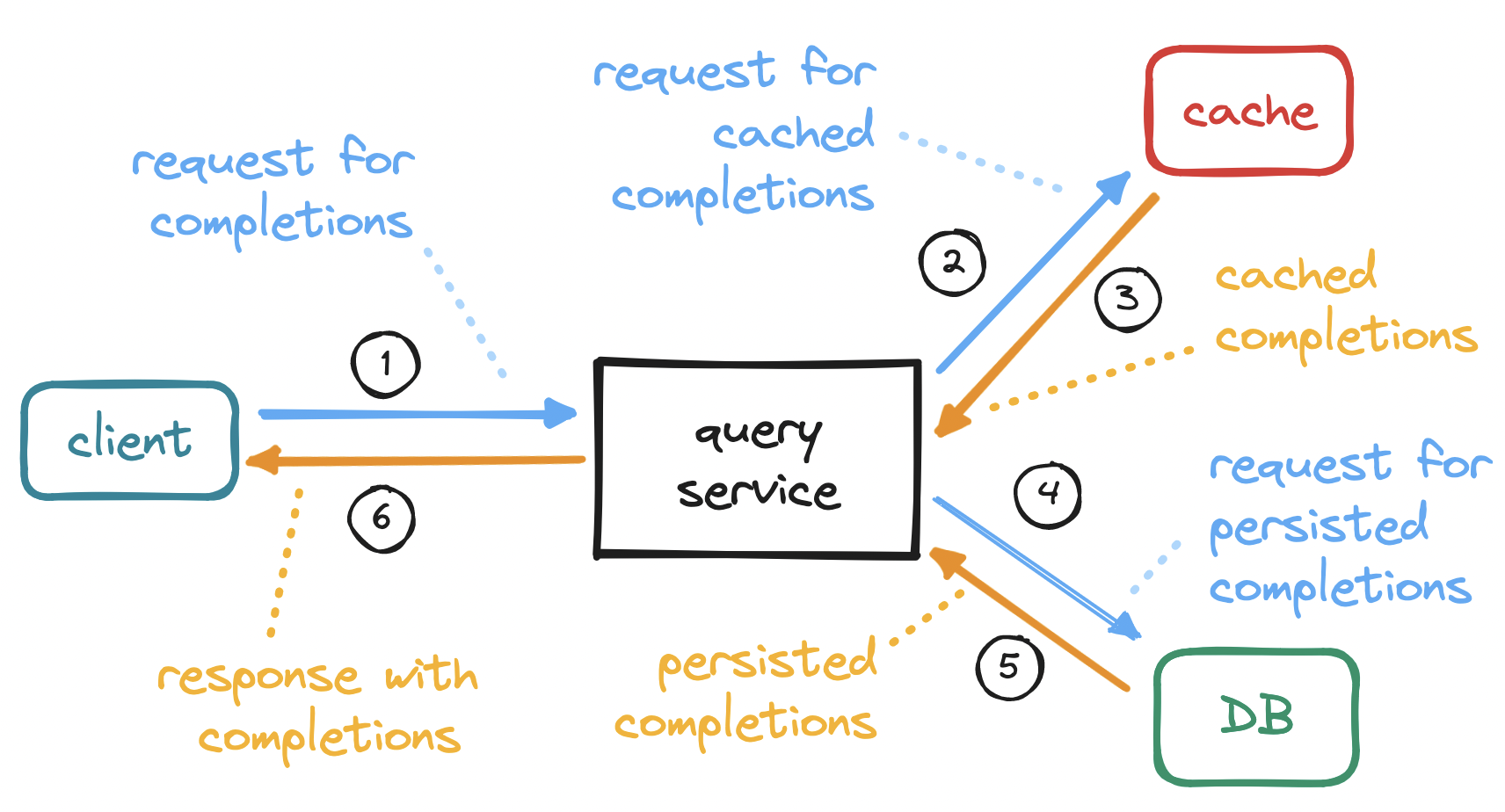
The high-level flow here is straightforward. On receiving a request, we query a cache (or on cache miss, persistent storage) and return relevant results, ensuring the cache is kept fresh. Given that so many of these interactions are common to other systems, we will center our discussion around the most distinctive aspect of typeahead search: the fast retrieval of suggestions relevant to user input.

Optimizing for reads

Think of our access pattern. In typeahead search, we query based on user input ("prefix") and our results must be semantically valid strings that follow from it ("completions"), sorted by frequency. The naivest solution might be a SQL query:

SELECT query_text, frequency FROM queries
WHERE query_text LIKE <prefix>%
ORDER BY frequency DESC;

While viable for small datasets, this SQL approach does not scale. Pattern matching with a wildcard causes inefficient range scans, and string comparisons are computationally expensive. As the dataset grows, our query will become slower and slower, so this approach is a non-starter.

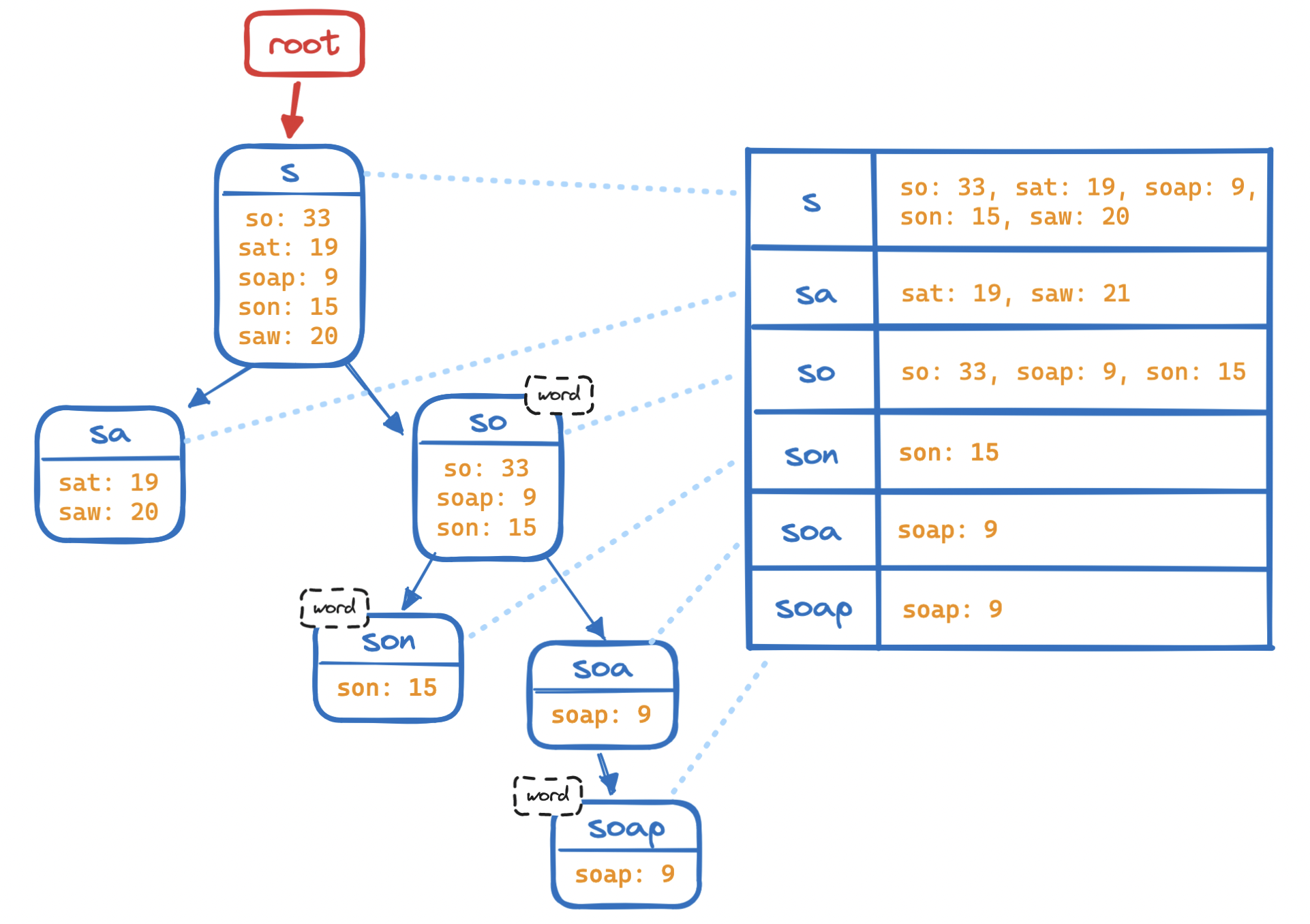
A more natural fit for text search is the trie, a data structure specialized in storing and finding strings in a vast collection. Typically, a trie is a tree where every node is home to a character, and where every child of a node holds a character that follows the character in the parent node, or the sequence up to that node.

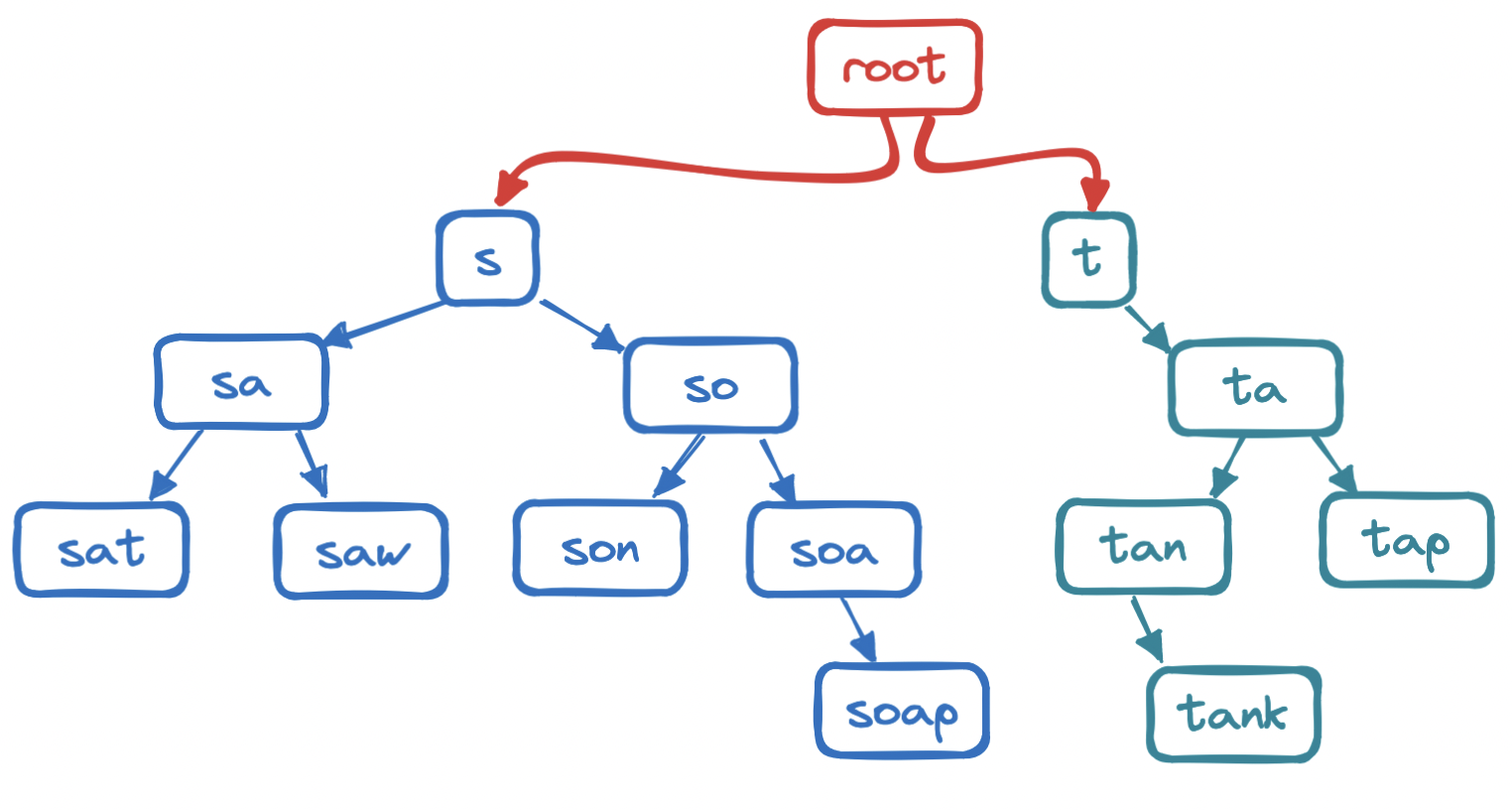
Each path from root to leaf represents a string, but not all strings are semantically valid. A string in a trie may be a stub like soa, a full word like soap, or a multi-word query like soap opera shows. (Note how whitespace is just another character.) To filter out invalid completions, we can mark the end of a semantically valid sequence of characters by flagging its terminal node. This terminal node is also a good spot to store the frequency of the string.

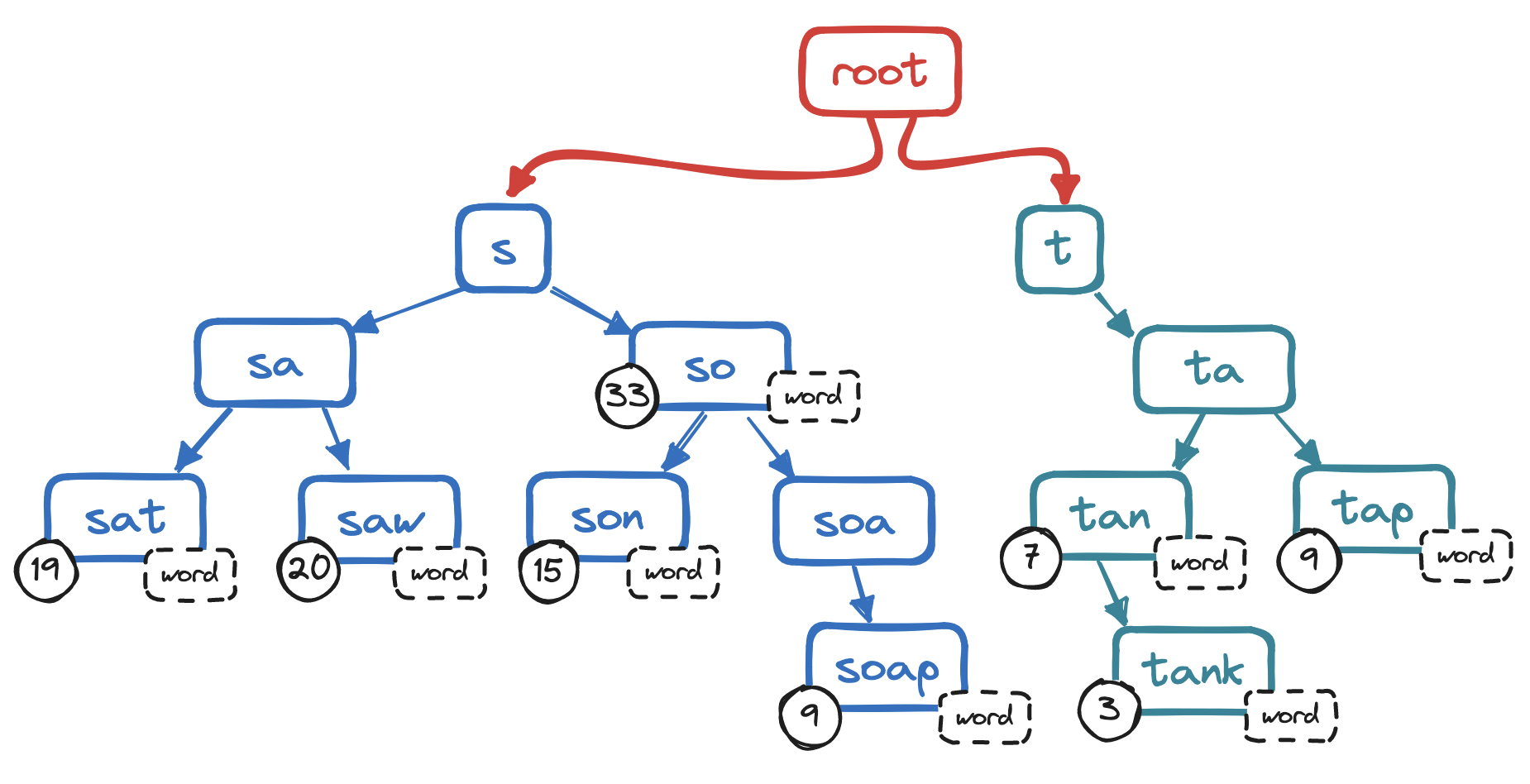
How does this help us? To retrieve a string based on user input ("prefix"), we need to traverse the trie until reaching the node that contains the final character of the prefix.

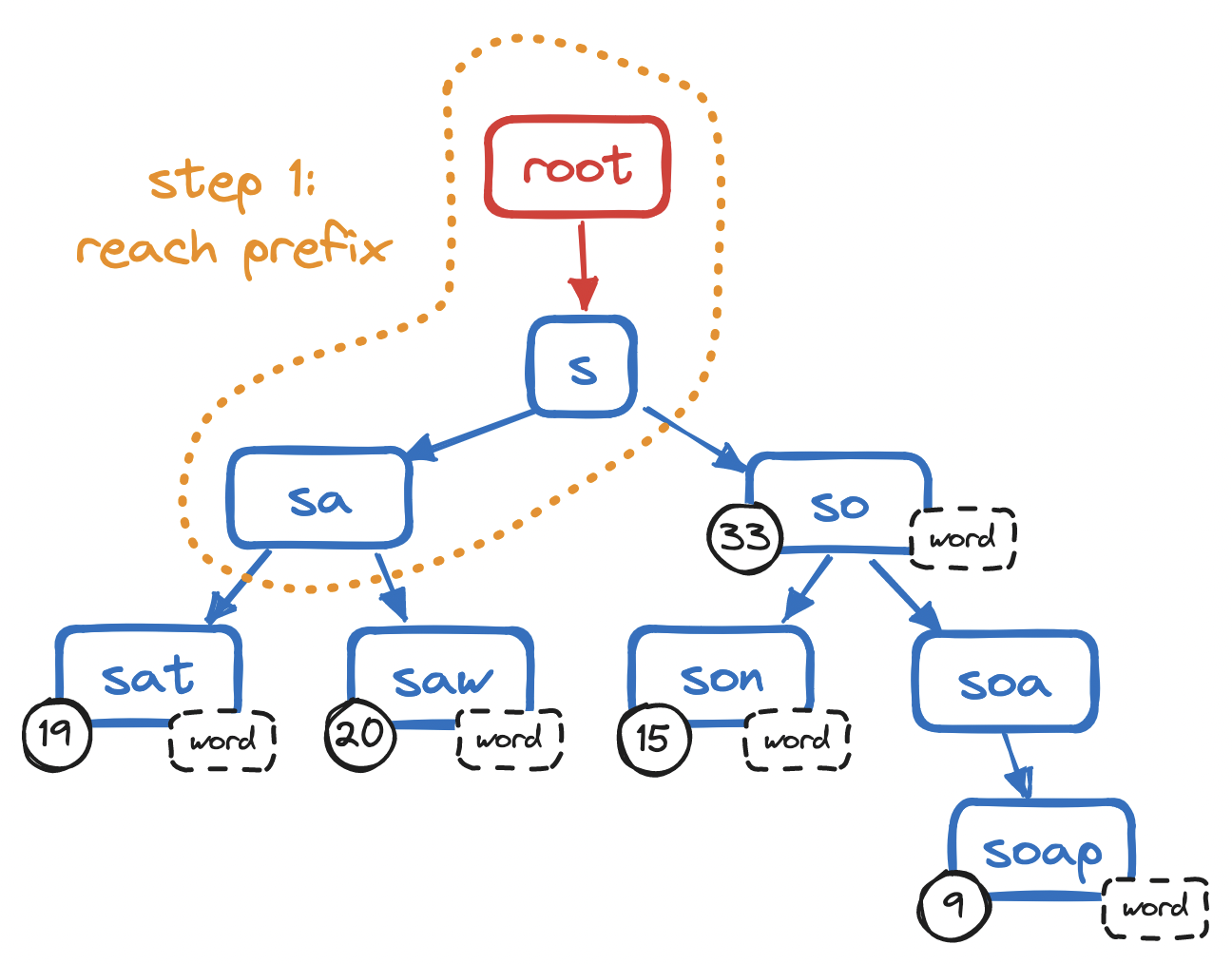
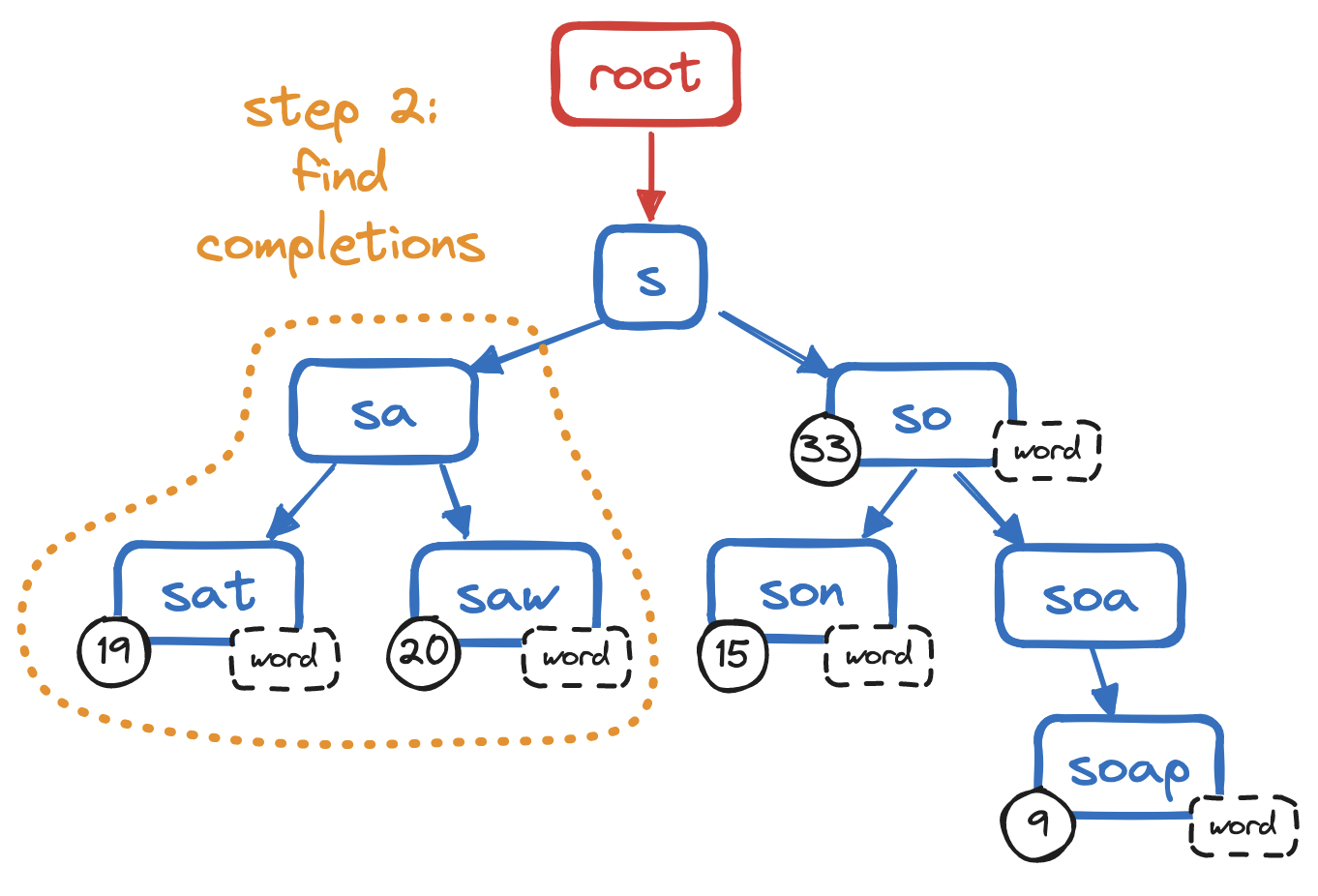
From there, we traverse the children of the prefix, i.e. we visit every child in this subtree, collecting all the strings ("completions") that start with the prefix.

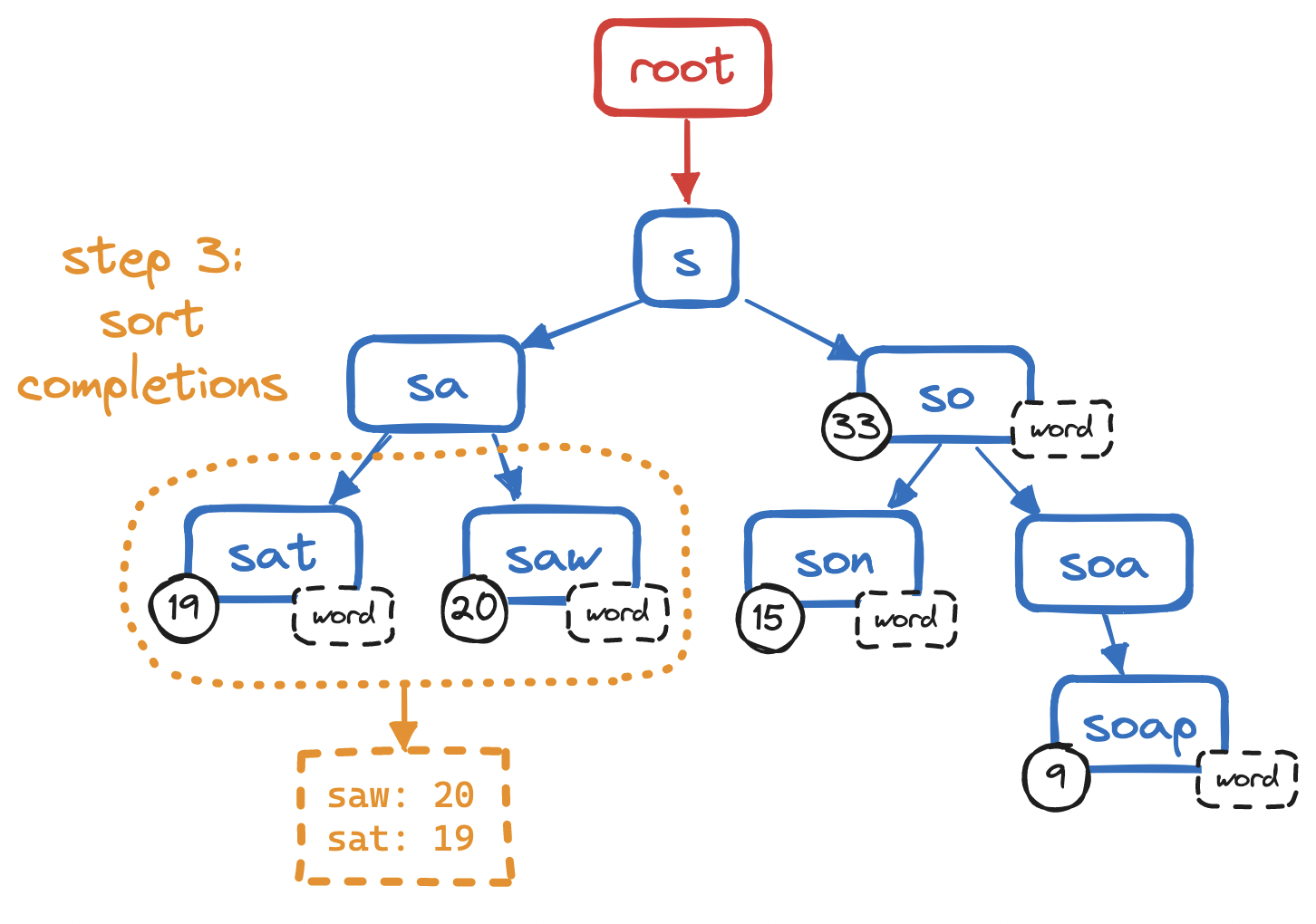
And finally, we sort the completions we found.

In other words, retrieval follows three steps:

1. Reach the end of the prefix: O(n)
2. Find all its completions: O(n) (worst case)
3. Sort the completions: O(log n)

Notice that this is an overall time complexity of O(n), which does not scale. Let's see how we can improve it step by step.

Consider the second step. Finding all completions is the most expensive step, and it will take longer and longer as the trie grows. To optimize this step, instead of storing a frequency value at each node, we can store all completions and their frequency values for a node at the node itself. In other words, all the information contained in the subtree is now at its root. Much less space-efficient, but we "trim" the tree—we do away with subtree traversals to find completions.

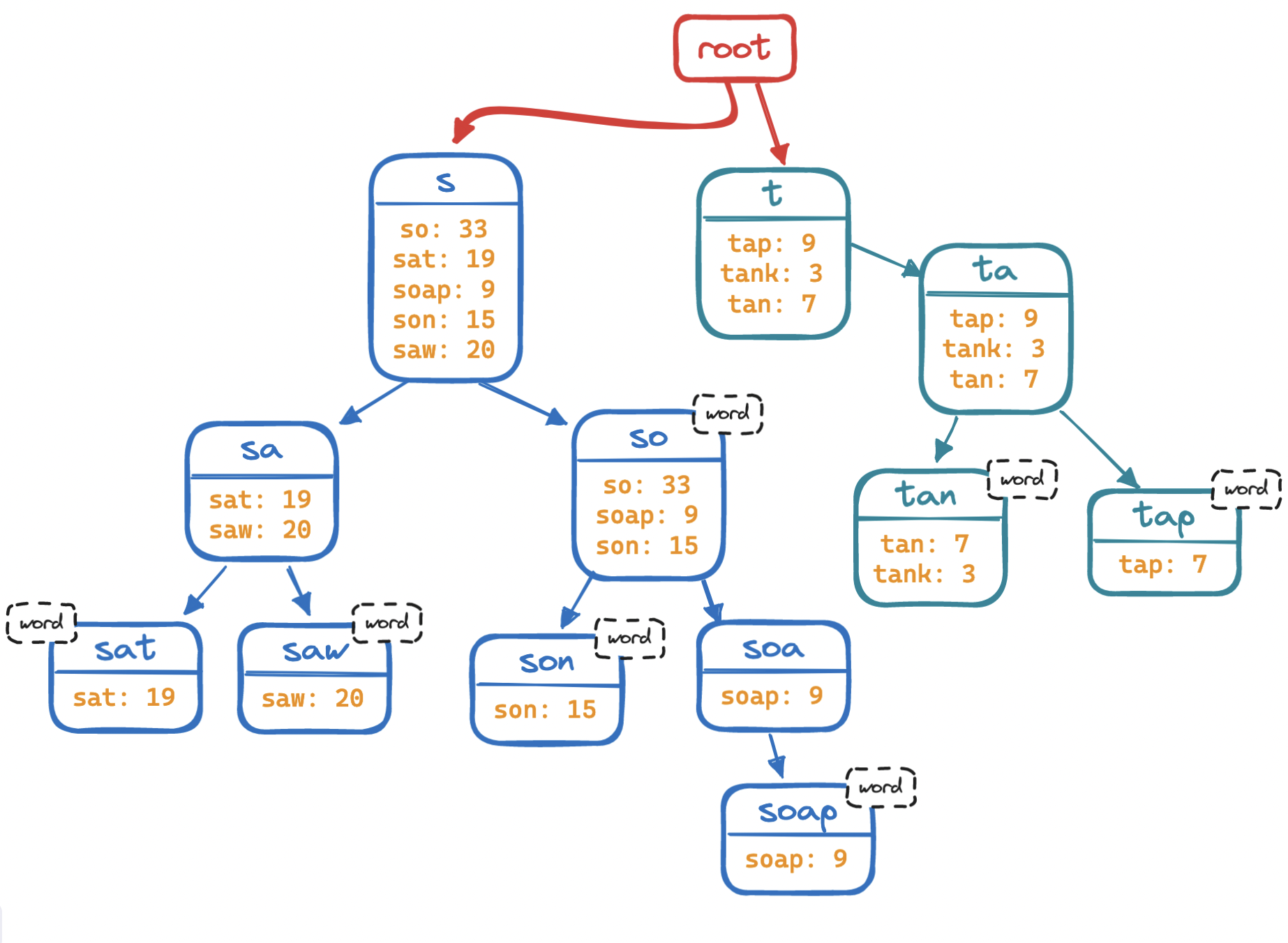
What about the first step? Reaching the end of the prefix is also O(n), if less expensive than traversing a subtree. It is reasonable to expect that a query is likely to be short, i.e. very long queries like soap opera shows that aired in 2020 in Turkey are statistically unlikely. There are diminishing returns to storing every single prefix for long-query cases, so we can choose to restrict prefix length. The shorter the prefix, the fewer nodes we will need to traverse.

Now look back at the third step. If it is reasonable to expect that a query is likely to contain only a handful of words, it is also reasonable to expect that a user is likely to only ever need a handful of suggestions, that is, not all children in the entire subtree. Hence, again, if we restrict the number of completions we store for a prefix, we will have less data we need to store and sort through.

In sum, by holding values constant, we have reduced time complexity from O(n) to O(1), which will scale nicely. Another improvement is in the data structure itself: rather than a regular trie, we can opt for a prefix hash tree, where every prefix is a hash key and completions are the value of that key. Depending on our requirements, we may choose to keep or outright discard semantically invalid strings.

This data structure grants us O(1) access to completions for any prefix, eliminating traversals altogether. Once again, we are trading space for speed of retrieval, but this is a tradeoff we are willing to make.

Storing our data structure

A prefix hash tree is also a perfect match for a key-value store. And given our use case, we would do well to look at an in-memory key-value store. Redis is a popular choice for typeahead search, being fast, simple and versatile, with native data structures to support our access pattern. Which Redis data structure best fits our use case?

In a Redis linked list, we can set up a chain of nodes where each holds a completion and its value, with all of them sorted by frequency and lexicographical order. To find completions, we can issue an LRANGE command to fetch the top n suggestions at the top of the list in O(1). And to add a completion, we can issue an RPUSH command to append it to the tail of the list in O(1). In both cases, the time complexity is stellar.

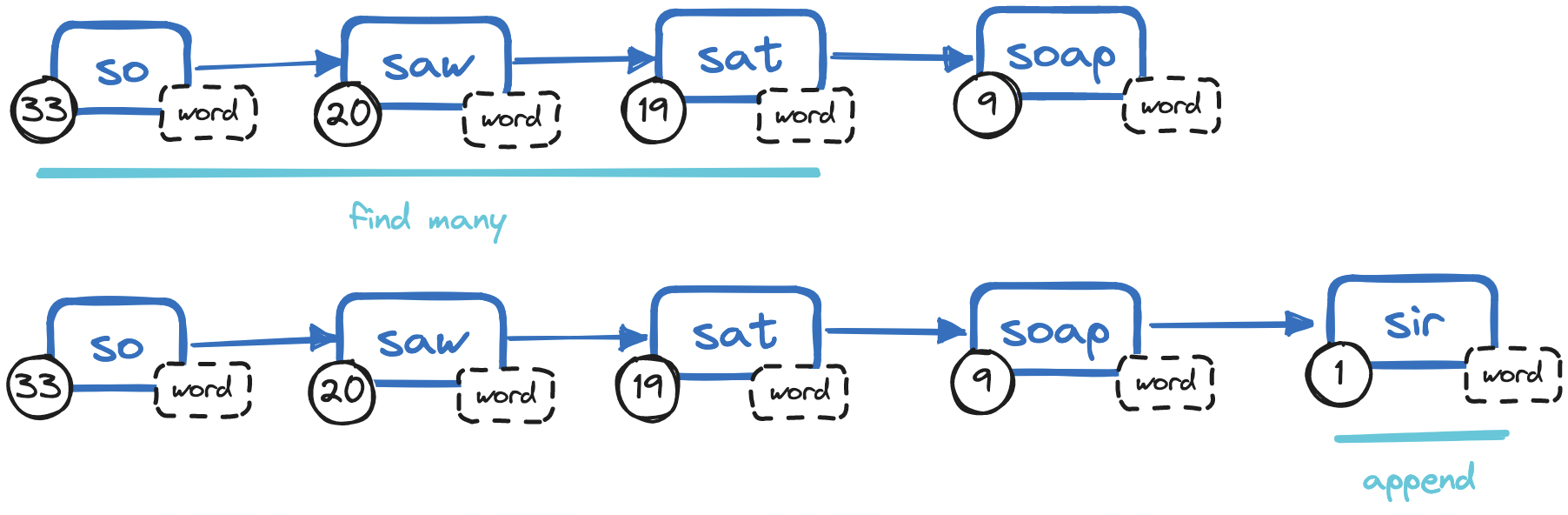
But updates pose a problem. To update a node to increment its frequency, we will need to remove it and re-insert it at its new position, a costly multi-step operation:

1. Retrieve the entire linked list: O(n)
2. Binary search the list to find the target node: O(log n)
3. Update the target node to increment its frequency: O(1)
4. Binary search the list to find the new position of the target node: O(log n)
5. Find and remove the target node from its current position: O(n)
6. Find and insert the target node at its new position: O(n)

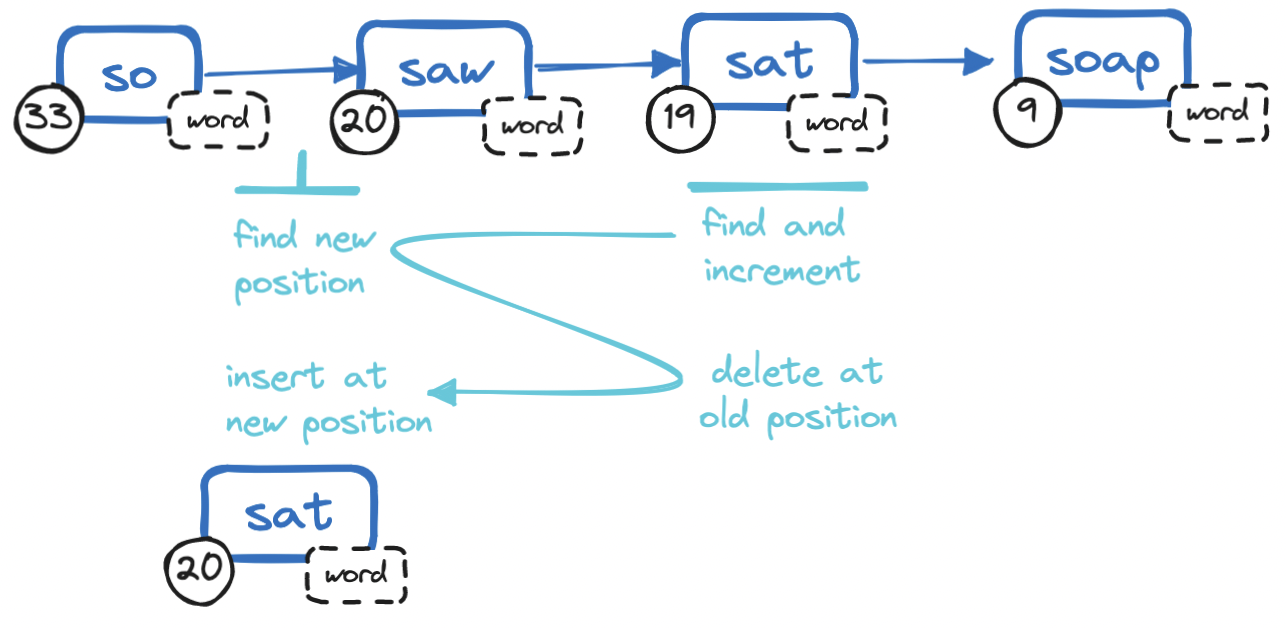
All this work is far from ideal:

• Overall time complexity is O(n).
• We are making more than one round trip to Redis.
• We are serving the entire list as a payload.
• Sorting occurs at the application level.
• Concurrent updates may become an issue.

In short, O(1) for search and addition is superb, but not at the cost of O(n) updates, not to mention that this is a poor match for a prefix hash tree. Can we do better?

In a Redis sorted set, for each letter in the alphabet, we can set up an ordered collection of items, each consisting of a string and a frequency value. Redis itself keeps the set in order (by frequency value and then by lexicographical order) and also takes care of deduplicating strings.

In a sorted set, retrieval is straightforward: Redis offers the ZRANGE command to retrieve the top n elements in O(log n). Likewise, to add to a sorted set, Redis offers ZADD, which is also O(log n). Both operations are slower than their linked list equivalents at O(1), while still relatively fast.

But where sorted sets shine is in update operations. Redis offers ZINCRBY to increment the score of a member in O(1), a significant improvement over linked lists, which requires O(n). Refer to the Redis documentation for details on the skip lists that make this possible.

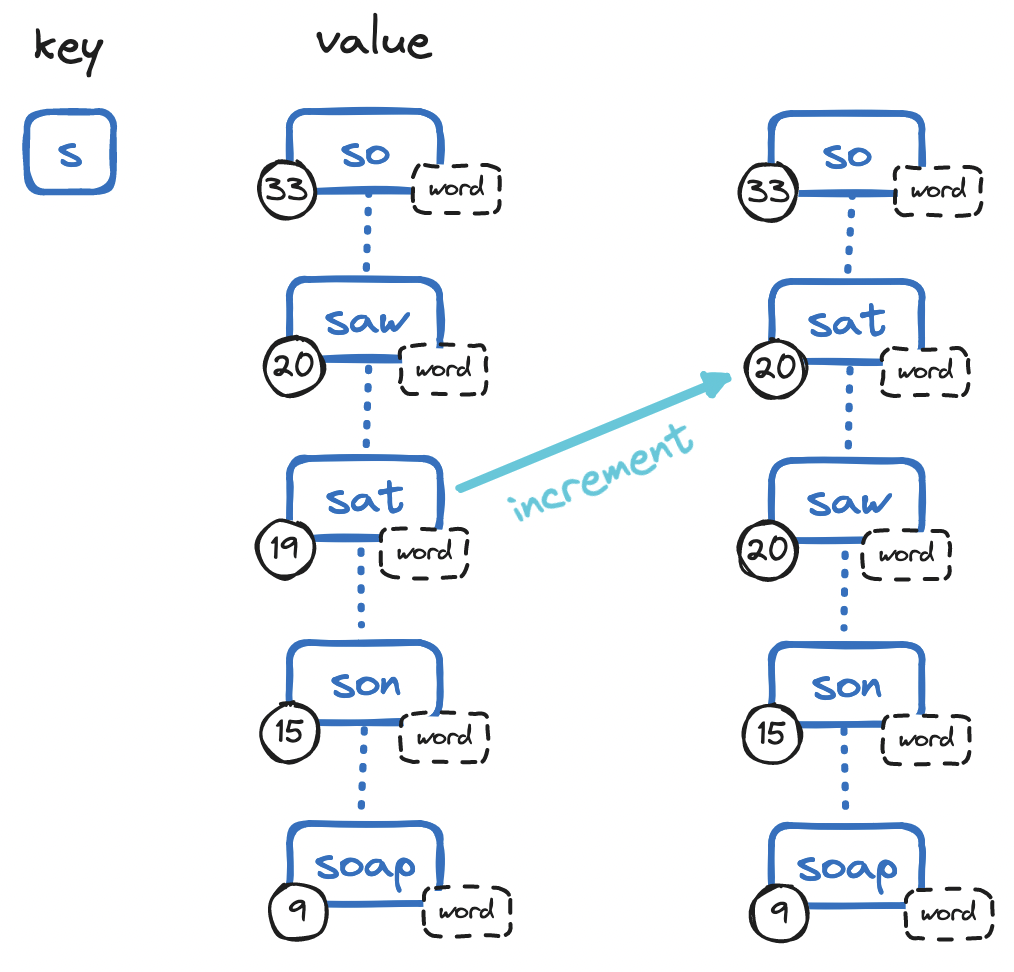
This option addresses most shortcomings of linked lists:

• Overall time complexity is O(log n).
• We are making only one round trip to Redis.
• We are serving only the top n elements as a payload.
• Sorting and deduplicating are delegated to Redis.
• Concurrent updates become less likely.

Sorted sets are therefore a better fit for our use case. But there is one pending issue.

Earlier we chose to limit the number of completions we store for a prefix. But doing so at the application level would mean retrieving the entire sorted set, removing the least frequent items, and storing the updated set. How do we enforce this limit in sorted sets? The creator of Redis himself offers an elegantly simple solution.

On adding a completion that causes the set to overstep the size limit:

1. Remove the completion with the lowest frequency, but store this value.
2. Add the new completion to the set, with the stored frequency value plus 1.

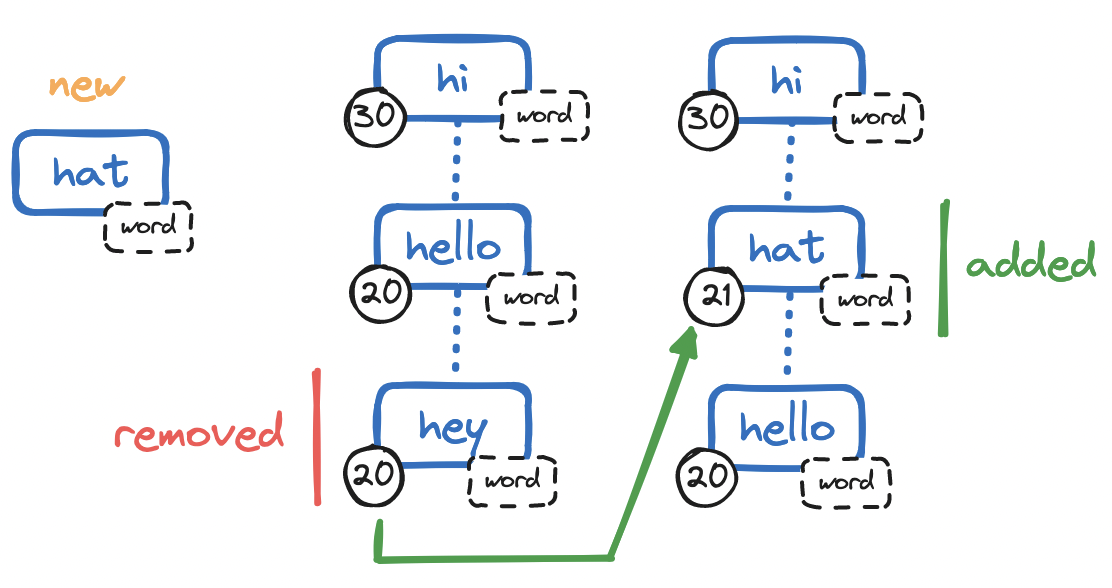
Why reuse the incremented frequency value for the new completion? If we were to add the new completion with a frequency of 1, the new completion would be the least relevant completion in the set—bound to be removed on the next addition—so this ensures the new completion will not be immediately replaced by the next completion. We afford all completions an equal opportunity to rise to the top.

Going further

In this discussion, we laid out a design for the retrieval component of a typeahead search system—zeroing in on optimizing queries, storing our data structure, and translating our choices to performant operations, while keeping an eye on tradeoffs and limitations. We paid careful attention to time complexity, which is essential for creating the search experience users have come to expect.

But this is only one aspect out of many. As our system grows, keeping all data in memory will soon become infeasible, i.e. we are likely to need persistent storage. In fact, when limiting our sorted set size, we might want to evict stale prefixes to persistent storage, rather than dropping them entirely.

To keep building out the system, consider:

• how to select a DB that maps well to our prefix hash tree,
• how to prime our cache and keep it up to date on cache miss,
• how to set up an ingestion and processing pipeline for our system,
• how to harness browser storage to cache completions, and
• how to debounce keypress events to prevent excess requests.

In designing a typeahead search system, remember that optimizing retrieval is only the beginning of a larger discussion where there is much more to explore.