Sort Algorithms

Bubble sort

On each pass:

1. loop over the array from left to right in pairs
2. if the items are out of order, swap them.

We need multiple passes to fully bubble sort the array. After each pass, the last unsorted item bubbles up to its correct position. In the best-case scenario, the array already sorted and requires only 1 pass; in the worst-case scenario, the array is sorted in reverse and requires n passes.

Operation	Best	Worst
Iteration	O(1)	O(n)
Comparison	O(n)	O(n)
Total	O(n)	O(n²)

Implementation

public void bubbleSort(int[] array) {

    // loop over each item in array
    for (var i = 0; i < array.length; i++) {

        // loop over each following item in array
        for (var j = 1 ; j < array.length; j++)

            // compare current item with following item
            // and if comparison yields unsorted, swap them
            if (array[j] < array[j-1])
                swap(array, j, j-1);
    }
}

// helper method
private void swap(int[] array, int index1, int index2) {
    var temp = array[index1];
    array[index1] = array[index2];
    array[index2] = temp;
}

First optimization: Do not sort if already sorted!

public void BubbleSort(int[] array) {
    boolean isSorted;

    // loop over each item in array
    for (var i = 0; i < array.length; i++) {
        isSorted = true;

        // loop over each following item in array
        for (var j = 1 ; j < array.length; j++)

            // compare current item with following item
            // and if comparison yields unsorted, swap them
            if (array[j] < array[j-1])
                swap(array, j, j-1);
                isSorted = false;

        if (isSorted)
            return;
    }
}

Second optimization: Do not compare items already in the correct position. Remember that, after each pass, the last unsorted item bubbles up to its correct position.

for (var j = 1 ; j < array.length - i; j++) {
    // ...
}

Selection sort

On each pass:

1. select the smallest item and swap it with the item at the first position
2. then the array is divided into a a sorted and unsorted part.

Subsequent passes also select the smallest item and swap it with the one at first position, in the unsorted part only.

Operation	Best	Worst
Iteration	O(n)	O(n)
Comparison	O(n)	O(n)
Total	O(n²)	O(n²)

Implementation

public void selectionSort(int[] array) {
    for (var i = 0; i < array.length; i++) {
        var minIndex = i;
        for (var j = i; j < array.length; j++) {
            if (array[j] < array[minIndex])
                minIndex = j;
            swap(array, minIndex, i);
        }
    }
}

var j = i because we should search starting from the unsorted part. Remember that we sort one item with each pass.

var minIndex = i; assumes that the first item in the unsorted part is the minimum.

With the findMinIndex section refactored:

public int findMinIndex(int i)  {
    var minIndex = i;
    for (var j = i; j < array.length; j++) {
        if (array[j] < array[minIndex])
            minIndex = j;
    return minIndex;
}

Insertion sort

Every time you get an item from an array, you insert it in the correct position. Instead of swapping items, insertion means shifting them to the right in the sorted part. As with selection sort, on every pass we build a sorted part and work only on the unsorted part.

Operation	Best	Worst
Iteration	O(n)	O(n)
Shifting	O(1)	O(n)
Total	O(n)	O(n²)

Implementation of insertion sort

public void insertionSort(int[] array) {
    for (var i = 1; i < array.length; i++) {
        var current = array[i];
        var j = i - 1;
        // compare current and existing item (j)
        while (j >= 0 && array[j] > current) {
            // shift existing item to the right
            array[j + 1] = array[j];
            j--;
        }
        // store current where existing item was
        // remember, you decreased j for this
        array[j + 1] = current;
    }
}

var i = 1; because we assume the item at index 0 is already in the correct position, because there are no other items we can compare a single item to.

Merge sort

Bubble sort, selection sort and insertion sort are inefficient, running in quadratic time.

Merge sort runs in O(n log n).

Merge sort: Break down the list into smaller and smaller sublists, sort those and merge them back to build a completely sorted list.

Creating smaller lists means allocating additional memory space for merge sort to run.

Procedure: Divide the array into half. Then, divide the first subarray by half into two subarrays. We divide recursively until we cannot divide anymore. Then merge the subarrays so that the resulting array is sorted.

Operation	Best	Worst
Dividing	O(log n)	O(log n)
Merging	O(n)	O(n)
Total time	O(n log n)	O(n log n)
Total space	O(n)	O(n)

Implementation

public void mergeSort(int[] array) {
    // base condition to terminate recursion
    // condition: array with single item
    // because array with single item is already sorted
    if (array.length < 2)
        return;

    // divide array into half
    var middle = array.length / 2;
    int[] left = new int[middle];
    for (var i = 0; i < middle; i++) {
        left[i] = array[i];
    }
    int[] right = new int[middle.length - middle];
    for (var i = middle; i < array.length; i++) {
        right[i - middle] = array[i];
    }

    // sort each half → recursion
    mergeSort(left);
    mergeSort(right);

    // merge results → recursion
    merge(left, right, array);
}

private void merge(int[] left, int[] right, int[] result) {
    // three indexes for iterating over each of the three arrays
    int i = 0, j = 0, k = 0;
    while (i < left.length && j < right.length) {
        if (left[i] <= right[j]) {
            result[k] = left[i];
            k++; // increment to store next in result
            i++; // increment to read next item in left
        } else {
            result[k] = right[j];
            k++; // increment to store next in result
            j++; // increment to read next item in right
        }
    }

    while (i < left.length)
        result[k++] = left[i++];


    while (i < left.length)
        result[k++] = right[j++];
}

We index with i - middle because we are looping starting from the middle and we need to store items starting at index 0 of right.

Quick sort

Select an item (a.k.a. "pivot") so that all items smaller than the pivot are on the left and all items larger than the pivot are on the right (a.k.a. "partitioning"). Then, in the left partition, pick another pivot and reorder around this new pivot. Then again, in the left partition do the same. This until we have a partition with a single item, which we know to be sorted.

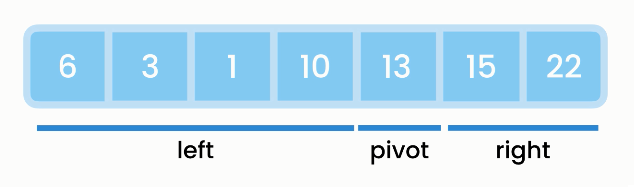
To partition, we use two variables, i to iterate over the array and b to mark the boundary of the left partition (a.k.a. "smaller numbers partition"). i of course starts at 0. b starts at -1 because at first the left partition is empty.

As we iterate over the array, if you find an item smaller than the pivot, you move the smaller number to the left partition and bring b forward.

Operation	Best	Worst
Partitioning	O(n)	O(n)
## of times	O(log n)	O(n)
Total time	O(n log n)	O(n²)
Total space	O(log n)	O(n)

Quick sort is similar to merge sort but quick sort requires less space. Quick sort also works in-place.

// start and end determine what part of the array we are trying to sort, example:
// 0, 9 → full array
// 4 → pivot
// 0, 3 → left partition
// 5, 9 → right partition

Remember, you're using D&C. So you want to break down this array until you're at the base case. Here's how quicksort works. First, pick an element from the array. This element is called the pivot.

Empty arrays and arrays with just one element will be the base case. You can just return those arrays as is—there's nothing to sort.

First, pick an element from the array. This element is called the pivot. Now find the elements smaller than the pivot and the elements larger than the pivot.

This is called partitioning. Now you have

• A sub-array of all the numbers less than the pivot
• The pivot
• A sub-array of all the numbers greater than the pivot

How do you sort the sub-arrays? Well, the quicksort base case already knows how to sort arrays of two elements (the left sub-array) and empty arrays (the right sub-array). So if you call quicksort on the two sub-arrays and then combine the results, you get a sorted array!

Here are the steps:

1. Pick a pivot.
2. Partition the array into two sub-arrays: elements less than the pivot and elements greater than the pivot.
3. Call quicksort recursively on the two sub-arrays.

The sub-arrays get sorted, and then you combine the whole thing to get a sorted array.

For quick sort, in the worst case, the stack size is O(n); in the best case, the stack size is O(log n).

If you're implementing quicksort, choose a random element as the pivot. The average runtime of quicksort is O(n log n)!

Implementation

Implementing quick sort in Java:

public void quickSort(int[] array, int start, int end) {
    // base condition to terminate recursion
    if (start >= end)
        return;

    // partition the array based on the pivot, assumed to be the last item of the array
    var boundary = partition(array, start, end);

    // get the position of the pivot, and then recursively sort the left and right partitions
    // note: `boundary -/+ 1` because boundary is the pivot
    // recursion
    quickSort(array, start, boundary - 1);
    quickSort(array, boundary + 1, end);
}

// return index of pivot after it has moved to its correct position
private int partition(int[] array, int start, int end) {
    var pivot = array[end] // last item of element we are working with
    var boundary = start - 1; // always one less than start of array

    for (var i = 0; i <= end; i++)
        if (array[i] <= pivot) // if item is smaller
            swap(array, i, ++boundary); // put it in left partition

    // boundary is now index of pivot after moving
    return boundary;
}

Counting sort

Bubble sort, selection sort, insertion sort, merge sort and quick sort are comparison-based algorithms. Counting sort, bucket sort and radix sort do not.

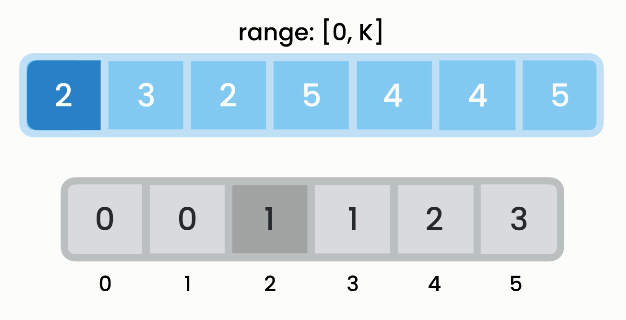
In counting sort, we iterate over input array, create a "counts" array, look at the first item, update the count item in the "counts" array at the corresponding index (if looking at item with value 5, update "counts" array at index 5 to 1).

read value X of item in input array → update count value at index X in "counts" array

Finally, we iterate over the "counts" array:

• if the count value of an item is 0, we skip it over;
• if the count value of an item is 1, we store its index (not the value) as a value in the first item of the result array;
• if the count value of an item is 2, we store its index (not the value) as the next two values in the next two items of the result array.

In summary, instead of using comparisons, we count the occurrences of items in the input array, and use those counts and their indexes to sort the array.

Operation	BigO
Populating counts	O(n)
Iterating over counts	O(k)
Total time	O(n)
Total space	O(k)

k is the maximum value in the input array.

Counting sort is much faster than comparison-based algos, but this speed comes at the cost of higher memory allocation. This is called "time-memory trade-off".

Requirements:

• extra space is not an issue
• values are positive integers
• most of the values are present (prevents many elements with zero count)

Implementation

public void countingSort(int[] array, int max) {
    int[] counts = new int[max + 1];
    for (var item : array)
        counts[item]++;

    var k = 0;
    for (var i = 0; i < counts.length; i++)
        for (var j = 0; j < counts.length; j++)
            array[k++] = i;
}

Bucket sort

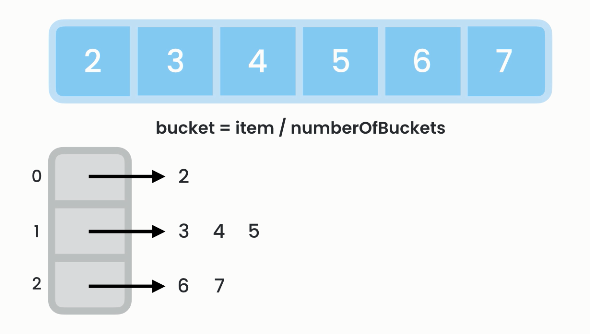
Bucket sort also dispenses with comparisons. Distribute items in a number of buckets, sort the items in each bucket using another sorting algorithm (unimportant implementation detail) and then combine them. The number of buckets affects performance.

Formula for determining which bucket to assign an item to:

• bucket = item / numberOfBuckets

Operation	Best	Worst
Distribution	O(n)	O(n)
Iterating over buckets	O(k)	O(k)
Sorting	O(1)	O(n²)
Total time	O(n + k)
Total space	O(n + k)

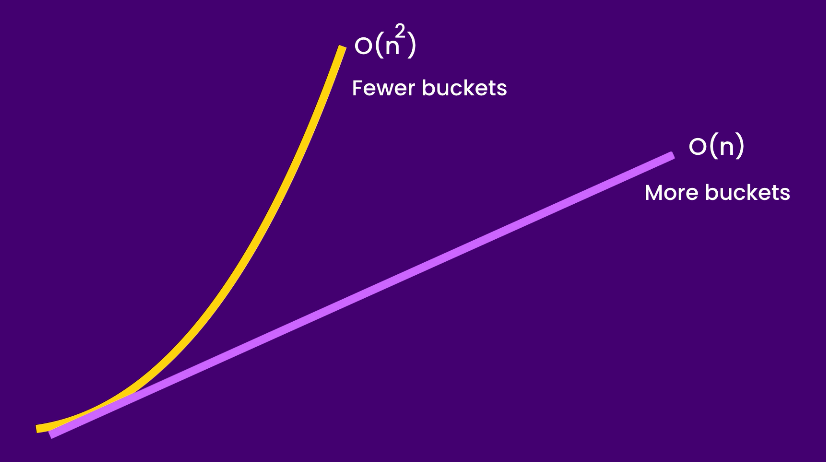
Time-memory tradeoff: More buckets (more memory) mean faster operation. Fewer buckets (less memory) mean slower operation.

Implementation

public void bucketSort(int[] array, int numberOfBuckets) {

    var buckets = createBuckets(array, numberOfBuckets);

    // distribute items among buckets
    var i = 0;
    for (var bucket : buckets) {
        Collections.sort(bucket);
        for (var item : bucket)
            array[i++] = item;
    }
}

private List<List<Integer>> createBuckets(numberOfBuckets, int[] array) {
    List<List<Integer>> buckets = new ArrayList<>();

    for (var i = 0; i < numberOfBuckets; i++)
        buckets.add(new ArrayList<>());

    for (var item : array)
        buckets.get(item / numberOfBuckets).add(item);

    return buckets
}